CS_SJ said:
Hello,
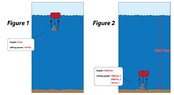
I'm a little confused about water pressure at extreme depths. Let's say that you attached a 100 lb. weight to a barrel, and the barrel had barely enough buoyancy to be able to just hold that weight at the surface (see Figure 1.)
Then, you took the same barrel and you put it at the bottom of the ocean 1000 feet down (see Figure 2) would the pressure down there give the barrel more lifting power? Would that same barrel be able to lift 1000 lbs. down there? 2000 lbs.?
Or, would the pressure on top of the barrel equal it all out and even 1000 feet down, all the barrel could lift is 100 lbs.?Extra question: if the barrel at the bottom of the ocean WOULD have more lifting power, does that mean it would accelerate like a rocket off of the bottom of the ocean, and then slow down the closer it got to the surface?
Thank you,
- DJ
I'm no expert but I have been scuba diving and using lift bags for recovery for 13 years so I feel I can add some useful information here in response to your question.
"Lift" (buoyancy) is primarily a function of displacement. "Pure" water weighs about 8 pounds per gallon, so for every 1 gallon (volume) of displacement, you will get 8 pounds of lift. This will not vary much, as shown in the density to depth graph posted by one responder. So, in your example, if you have 100 pounds of positive buoyancy at the surface, the difference in lift of the same displacement of water at 1,000 feet depth or 10,000 feet depth, will be negligible. This assumes that the lift vessel is rigid meaning that the displacement of water doesn't change with ambient pressure (depth in the water column).
As for acceleration: This is dependent on the type of displacement you have: variable or fixed. It will not be caused by the "extra" lift the vessel has at the bottom but by the expansion of the air in the vessel if it is allowed to expand as it rises in the water column. If you could displace 100 pounds of water, you would have 100 pounds of "lift" (minus the weight of the displacing vessel). If the vessel is rigid and sealed (fixed displacement), the amount of lift would not vary other than by the variance in the density of the water which, again, isn't much based on pressure (depth).
This means the vessel must be able to resist the ambient pressure at whichever depth you're referring to (whether by structural integrity or by pressurization inside the vessel). The rate of rise would be fairly consistent other than the acceleration which occurs as the inertia of the masses involved are overcome until the terminal velocity is attained (the maximum velocity that the lift is able to move the objects through the water or the balance of the lift force countered by the gravitational pull on them).
If the lift vessel (displacing vessel) is variable (either flexible or has an opening at the bottom) which allows air inside to be compressed or to expand, then the lift force of 100 pounds at the surface will be reduced as depth in the water column (pressure) is increased (the air is compressed and the displacement is reduced). If you have access to a swimming pool or other body of water clear enough to see well in, you can take a glass bottle, fill it with air, hold it opening-side down, and descend in the water column and watch the air consume less and less volume inside the bottle the deeper you take it. As the air is compressed, it takes up less volume.
As *displacement* of water is the determining factor, in this simplified example, for lift, the less volume occupied, the less lift provided. In this example, you can fill the bottle with just enough air to keep it on the surface and then take it down the water column, allowing the air inside to be compressed. If the positive buoyancy is sufficiently small, and the water column deep enough, at some point the air will be compressed enough as to no longer provide enough lift to keep the bottle positively buoyant at which point it will begin to sink. The further it sinks, the greater the ambient water pressure, the less the "lift" force by the displacement of the air because the air is compressed more.
Conversely, as for acceleration of lift, if you fill the bottle with water at some depth, say 15 feet for example, and then fill it with just enough air for the bottle to become slightly positively buoyant (opening down) and let it go, rising in the water column, the air inside will expand under the reduced ambient pressure. As the air increases in volume (becomes less compressed), so, too, does the lift increase. The rate of rise will increase, the rate of expansion will increase, and it's a cycle; faster and faster until the bottle gets to the top of the water column or the air expands so much that it begins to escape the vessel (or the bottle tumbles or the terminal velocity of an empty bottle in the water is reached).
It's not the best explanation I'm sure, but it's pretty good and it's accurate enough for understanding the basic principles. I've floated many a beer bottle from the bottom of a lake while scuba diving, playing with this phenomenon, watching a bottle ever so slowly begin to rise and then accelerate until it's out of sight.
HTH.
--HC
