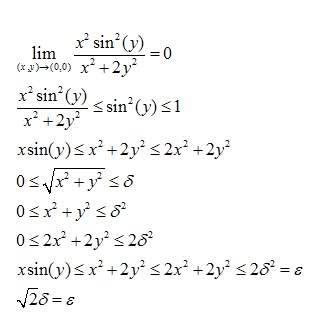SUMMARY
The limit of the expression x² * sin²(y) / (x² + 2y²) as (x,y) approaches (0,0) is definitively 0, proven using the delta-epsilon method. The approach involves selecting a small epsilon value, such as 0.1, and determining if the expression remains less than epsilon when (x,y) is within delta of (0,0). This iterative process helps confirm the correctness of the chosen delta. The discussion emphasizes the importance of validating the delta selection through testing with smaller epsilon values.
PREREQUISITES
- Understanding of limits in calculus
- Familiarity with the delta-epsilon definition of limits
- Basic knowledge of trigonometric functions, specifically sine
- Ability to manipulate algebraic expressions
NEXT STEPS
- Study the delta-epsilon definition of limits in depth
- Practice solving limits using the delta-epsilon method
- Explore the behavior of trigonometric functions near zero
- Learn about multivariable limits and their applications
USEFUL FOR
Students studying calculus, mathematics educators, and anyone seeking to understand the delta-epsilon method for proving limits in multivariable functions.