Limit Points & Closure in a Topological Space .... Singh, Theorem 1.3.7

[Math Amateur]

TL;DR

I am reading Tej Bahadur Singh: Elements of Topology, CRC Press, 2013 and am focused on the notions of limit points and closure in a topological space ... and I need help with understanding Singh's proof of Theorem 1.3.7 ...

I am reading Tej Bahadur Singh: Elements of Topology, CRC Press, 2013 ... ... and am currently focused on Chapter 1, Section 1.2: Topological Spaces ...

I need help in order to fully understand Singh's proof of Theorem 1.3.7 ... (using only the definitions and results Singh has established to date ... see below ... )

Theorem 1.3.7 reads as follows:

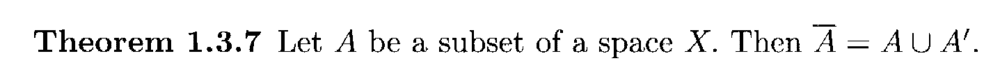
In the above proof by Singh we read the following:

" ... ... So $U$ is contained in the complement of $A \cup A'$, and hence $A \cup A'$ is closed. It follows that $\overline{A} \subseteq A \cup A'$ ... ... "My question is as follows:

Why does $U$ being contained in the complement of $A \cup A'$ imply that $A \cup A'$ is closed ... and further why then does it follow that $\overline{A} \subseteq A \cup A'$ ... ... Help will be appreciated ...

Peter==========================================================================================It is important that any proof of the above remarks only rely on the definitions and results Singh has established to date ... namely Definition 1.3.3, Proposition 1.3.4, Theorem 1.3.5 and Definition 1.3.6 ... which read as follows ... :

Hope that helps ...

Peter

 

[Infrared]

Let $Z=A\cup A'.$ Showing that every element of $X\setminus Z$ has an open neighborhood disjoint from $Z$ means that $X\setminus Z$ is open, that is, $Z$ is closed.

For your second question, we know $A\subseteq A\cup A'$. Taking closures of both sides gives $\overline{A}\subseteq \overline{A\cup A'}=A\cup A.'$ I am using the fact that if $B\subseteq C,$ then $\overline{B}\subseteq\overline{C}.$

 

[Math Amateur]

Let $Z=A\cup A'.$ Showing that every element of $X\setminus Z$ has an open neighborhood disjoint from $Z$ means that $X\setminus Z$ is open, that is, $Z$ is closed.

For your second question, we know $A\subseteq A\cup A'$. Taking closures of both sides gives $\overline{A}\subseteq \overline{A\cup A'}=A\cup A.'$ I am using the fact that if $B\subseteq C,$ then $\overline{B}\subseteq\overline{C}.$

Thanks for the help Infrared ... but can you help further ...

In showing $Z=A\cup A'$ is closed you write ... "Showing that every element of $X\setminus Z$ has an open neighborhood disjoint from $Z$ means that $X\setminus Z$ is open, that is, $Z$ is closed."

Can you explain homework this follows from the definitions and results Singh has established to date (which are Definition 1.3.3, Proposition 1.3.4, Theorem 1.3.5 and Definition 1.3.6 details of which are shown in my post ... note that the only relevant definitions and results Singh has established up to this point are the definition of a topology ... and hence an open set ... and the definition of a neighbourhood ... )

Hope you can help further ...

Peter

 

[Infrared]

The argument you quoted shows that for every $x\in X\setminus Z$, there is an open set $U_x\subset X\setminus Z$ that contains $x$. So we can write $X\setminus Z=\bigcup_{x\in X\setminus Z} U_x.$ This is a union of open sets, so $X\setminus Z$ is open. This means $Z$ is closed.

 

[Math Amateur]

Thanks Infrared ...

Really appreciate your help...

Peter