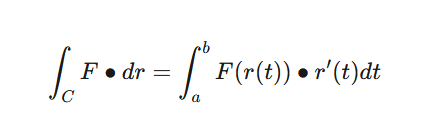Homework Help Overview
The discussion revolves around solving a line integral along a specified curve γ within the context of vector fields. Participants are exploring the complexities of substitutions and the potential path independence of the integral.
Discussion Character
- Exploratory, Assumption checking, Conceptual clarification
Approaches and Questions Raised
- Participants are attempting to apply relations for line integrals but find the substitutions challenging. Questions about the relationship between components of the vector field and the possibility of the field being conservative are raised. Some suggest comparing terms in expressions to glean insights.
Discussion Status
The discussion is ongoing, with participants providing guidance on examining the vector field's properties and suggesting checks for path independence. Multiple interpretations of the problem are being explored, particularly regarding the conservative nature of the field.
Contextual Notes
Participants mention the importance of start and end coordinates for the path and express uncertainty about the complexity of the problem. There are references to specific terms and derivatives within the vector field that may influence the approach taken.
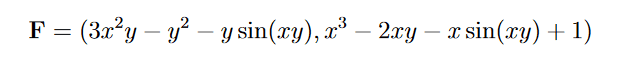
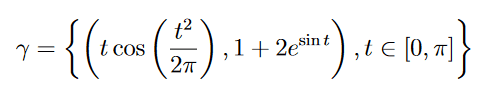 I attempt to apply this relation but the substitutions get too messy.
I attempt to apply this relation but the substitutions get too messy.