Line perpendicular to the ray

[Poetria]

Homework Statement

[/B]
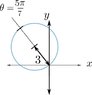
Consider the line whose shortest distance to the origin is 5 and that is perpendicular to the ray $\theta= \frac {5*\pi}{7}$ for r>0
Find its polar equation $r=r(\theta)$ and $\theta_1<\theta_2$ in the interval $[0, 2\pi]$ such that $r(\theta)\geq 0$ for all $\theta_1\leq\theta\leq\theta_2$ as $\theta$ increases from $\theta_1$ to $\theta_2$, the point $(r(\theta), \theta)$ traces the entire line once.

2. The attempt at a solution

m*x+b=y
$m=\tan(3/14*\pi)$
b=5/cos(2/7*pi)

$$-\frac{\frac 5 {\cos(\frac 2 7*\pi)}}{(\tan( \frac 3 {14}*\pi)*\cos(\theta)-\sin(\theta))}$$

 

[mjc123]

You have calculated b incorrectly. If you correct this, then your final answer will be right - but it's a long way round and a complicated expression. Try doing it without going through y = mx + b. Draw the ray, the line, and a point (r,θ) on the line. Can you derive a simpler expression for r(θ)?

 

[Poetria]

You have calculated b incorrectly. If you correct this, then your final answer will be right - but it's a long way round and a complicated expression. Try doing it without going through y = mx + b. Draw the ray, the line, and a point (r,θ) on the line. Can you derive a simpler expression for r(θ)?

Something like:

$r=5*sec(\theta-\frac 5 7*\pi)$

 

[mjc123]

That's what I got.

 

[Poetria]

That's what I got.

Great. :) Many thanks. :)

 

[SammyS]

Great. :) Many thanks. :)

Did you find $\ \theta _1\$ and $\ \theta _2\$ ?

 

[Poetria]

Did you find $\ \theta _1\$ and $\ \theta _2\$ ?

Yes, this was easy:
$$\theta_1=\frac 3 {14}\pi$$
$$\theta_2=\frac {17}{14}\pi$$