Hmm, that can't be true, since e_3 = (0, 0, 1) in the standard basis. Remember we are going to rotate this vector counterclockwise in the yz-plane, so its image after the transformation will be a different vector. Just to make sure we're on the same page, the standard basis is e_1 = (1, 0, 0), e_2 = (0, 1, 0), and e_3 = (0, 0, 1).
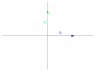
Now, the first attached image is meant to be a viewpoint where the positive x-axis, and thus e_1, is pointing out of the page. So we cannot see the x-axis from this viewpoint: it is directly above the origin of the yz-plane. The positive z-axis, and thus e_3 = (0, 0, 1) points right, while the positive y-axis, and thus e_2 = (0, 1, 0) points up. The diagram shows the counterclockwise direction of the rotation by 90 degrees and its magnitude.
The second illustration shows that when we rotate e_3 counterclockwise by 90 degrees in this plane, it coincides with e_2. So the components of the new vector T(e_3) are (0, 1, 0). Does that make sense so far?