Linear independence of Coordinate vectors as columns & rows

[CGandC]

Summary:: x

Question:

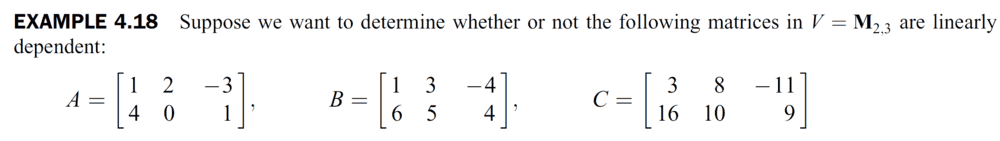
Book's Answer:

My attempt:

The coordinate vectors of the matrices w.r.t to the standard basis of $M_2(\mathbb{R})$ are:

$\lbrack A \rbrack = \begin{bmatrix}1\\2\\-3\\4\\0\\1 \end{bmatrix} , \lbrack B \rbrack = \begin{bmatrix}1\\3\\-4\\6\\5\\4 \end{bmatrix} , \lbrack C \rbrack = \begin{bmatrix} 3\\8\\-11\\16\\10\\9 \end{bmatrix}$
Putting these coordinate vectors in a matrix ( representing a homogeneous system of equations ):$\begin{bmatrix} 1 & 1 & 3 & | 0 \\ 2 & 3 & 8 & | 0 \\ -3 & -4 & -11 & | 0 \\ 4 & 6 & 16 & | 0 \\ 0 & 5 & 10 & | 0 \\ 1 & 4 & 9 & | 0 \\ \end{bmatrix}$

After many row operations I get the matrix:

$\begin{bmatrix} 1 & 0 & 0 & | 0 \\ 0 & 1 & 0 & | 0 \\ 0 & 0 & 1 & | 0 \\ 0 & 0 & 0 & | 0 \\ 0 & 0 & 0 & | 0 \\ 0 & 0 & 0 & | 0 \\ \end{bmatrix}$

[Moderator's note: moved from a technical forum.]

Clearly we have 3 leading coefficients, three of them in the first 3 rows, therefore the coordinate vectors $\lbrack A \rbrack , \lbrack B \rbrack , \lbrack C \rbrack$ are linearly independent, therefore the matrices $A , B , C$ are linearly independent.

Why am I getting a contradiction to the real answer ( that $A , B , C$ are linearly dependent )? How I could've a-priori known to represent the coordinate vectors as rows?

Is there a connection to column and row spaces?

 

[Office_Shredder]

It doesn't matter if you represent them as rows or columns. You made a mistake in the work that you did, can you post it?

 

[CGandC]

Turns out I made a mistake in the row operations ( even though I checked beforehand couple of times ), so I get the matrix:

$\begin{bmatrix} 4 & 6 & 16 & | 0 \\ 0 & 5 & 10 & | 0 \\ 0 & 0 & 0 & | 0 \\ 0 & 0 & 0 & | 0 \\ 0 & 0 & 0 & | 0 \\ 0 & 0 & 0 & | 0 \\ \end{bmatrix}$
So the coordinate vectors are clearly linearly dependent.

I have another question: Is there some theorem stating that it won't matter to represent the vectors as columns or rows in order to check linear dependence?