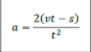rbh
- 9
- 1
- Homework Statement
- Motorcyclist is driving straight, horizontal road and then he starts to brake, within 2 seconds he travelled half the braking distance. Calculate how much time it took him to travell full braking distance.
- Relevant Equations
- d = (Vf^2 - Vi^2) / 2a
Vf = Vi + at
I tried using equations listed above to get the answer, but I get stuck with a and Vi. What am I doing wrong?
The answer is 6.7 seconds.
The answer is 6.7 seconds.