Discussion Overview
The discussion revolves around the stability analysis of a linear system represented by matrices, including an integral block. Participants explore methods to determine if the system is asymptotically stable, stable, or unstable, focusing on the implications of using matrix blocks in the system's representation.
Discussion Character
- Homework-related
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
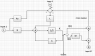
- The original poster questions how to analyze a system with matrix blocks and an integral block, expressing uncertainty about the appropriate methods for stability analysis.
- Some participants suggest posting the matrix block for clarity and inquire about the specific elements of the matrices involved.
- One participant explains the state space representation of the system, detailing the roles of matrices A, B, C, and D in determining stability.
- Another participant emphasizes the importance of finding the eigenvalues of the A matrix to assess stability, noting that stability is determined by whether these eigenvalues lie in the left half of the complex plane.
- There is a discussion about the dimensions of the matrices and how they relate to the inputs and outputs of the system.
- One participant provides specific values for the matrices involved and questions how these values might affect system stability.
- Participants discuss the implications of feedback and how it alters the stability analysis, suggesting that the original A matrix may need to be adjusted to account for additional inputs and feedback mechanisms.
- There are mentions of simplification techniques and whether they apply to matrix systems, with some participants expressing uncertainty about the legality of certain manipulations.
- One participant shares a trick regarding the stability of systems with zero non-diagonal elements in the A matrix, illustrating how to identify poles directly from the diagonal elements.
Areas of Agreement / Disagreement
Participants express a range of views on how to approach the stability analysis, with no clear consensus on the best method. Some agree on the importance of eigenvalues, while others raise questions about the representation and simplification of the system.
Contextual Notes
There are unresolved questions regarding the correct representation of matrix operations and the implications of feedback on stability. Participants also highlight the need for clarity in the system diagram and the definitions of various components.