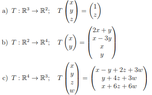Linear Transformations: Proving Rules & Demonstration

[Ereisorhet]

Good afternoon people.
So i have to demonstrate that the problems below are Linear Transformations, i have searched and i know i have to do it using a couple of "rules", it is a linear transformation if:
T(u+v) = T(u) + T(v) and T(Lu) = LT(u), the thing is that i really can't understand how to develop that and find the demonstration.
Thanks for reading.

View attachment 9033

 

[HallsofIvy]

For (a), let $$u= \begin{pmatrix}u_1 \\ u_2 \\ u_3\end{pmatrix}$$ and $$u= \begin{pmatrix}v_1 \\ v_2 \\ v_3\end{pmatrix}$$.

We are told that "$$T\begin{pmatrix}x \\ y \\ z \end{pmatrix}= \begin{pmatrix}1 \\ z \end{pmatrix}$$ so $$Tu= \begin{pmatrix}1 \\ u_3\end{pmatrix}$$ and $$Tv= \begin{pmatrix}1 \\ v_3\end{pmatrix}$$. So $$Tu+ Tv= \begin{pmatrix}2 \\ u_3+ v_3 \end{pmatrix}$$.
But $$u+ v= \begin{pmatrix}u_1+ v_1 \\ u_2+ v_2 \\ u_3+ v_3 \end{pmatrix}$$ so $$T(u+ v)= \begin{pmatrix}1 \\ u_3+ v_3\end{pmatrix}$$. Is T(u+ v)= Tu+ Tv?

For (b), let $$u= \begin{pmatrix}u_1 \\ u_2 \end{pmatrix}$$ and $$v= \begin{pmatrix}v_1 \\ v_2 \end{pmatrix}$$. $$Tu= \begin{pmatrix} 2u_1+ u_2 \\ u_1- 3u_2 \\ u_1 \\ u_ 2 \end{pmatrix}$$ and $$Tv= \begin{pmatrix} 2v_1+ v_2 \\ v_1- 3v_2 \\ v_1 \\ v_2 \end{pmatrix}$$. So $$Tu+ Tv= \begin{pmatrix}2u_1+ u_2+ 2v_1+ v_2 \\ u_1- 3u_2+ v_2- 3v_2 \\ u_1+ v_2 \\ u_2+ v_2 \end{pmatrix}$$.
$$u+ v= \begin{pmatrix}u_1+ v_1 \\ u_2+ v_2 \end{pmatrix}$$ so $$T(u+ v)= \begin{pmatrix}2(u_1+ v_1)+ (u_2+ v_2) \\ (u_1+ v_1)- 3(u_2+ v_3) \\ u_1+ v_1 \\ u_2+ v_2 \end{pmatrix}$$.

Do you see that those are the same, so T(u+ v)= Tu+ Tv?

Now we need to show that "T(Lu)= LTu" where L is a "scalar" (a number). $$Lu= \begin{pmatrix}Lu_1 \\ Lu_2 \end{pmatrix}$$ so $$T(Lu)= \begin{pmatrix} 2Lu_1+ Lu_2 \\ Lu_1- 3Lu_2 \\ Lu_1 \\ Lu_2 \end{pmatrix}$$ and $$LTu= L\begin{pmatrix}2u_1+ u_2 \\ u_1- 3u_2 \\ u_1 \\ u_2\end{pmatrix}= \begin{pmatrix}L(2u_1+ u_2) \\ L(u_1- 3u_2) \\ Lu_1 \\ Lu_2 \end{pmatrix}$$. Do you see that T(Lu)= LTu?