Linearizing a circuit with a nonlinear element

[zenterix]

Homework Statement

Consider the circuit containing the nonlinear element $N$ as shown below in Figure 3.

The $i-v$ relation fro the element $N$ is

$$i_A=(10\mathrm{A}(1-e^{-v_A/5\mathrm{V}})$$

(a) Write an equation which relates voltage $V_A$ to input voltage $v_I$.

(b) Solve for voltate $v_A$ when $v_I=\mathrm{10V}$.

(c) Find the incremental change in $v_A$ for a $2%$ increase in $v_I$ and calculate the ratio $\Delta v_A/\Delta v_I$.

(d) Find the value for the incremental resistance of the nonlinear element $N$ by linearizing the expression for $i_A$ about the operating point when $v_I=\mathrm{10V}$.

(e) Draw the incremental circuit model for the circuit shown in Figure 3.

(f) Find the ratio $\Delta v_A/\Delta v_I$ from the incremental circuit model and compare it with your exact model from part (c).

Relevant Equations

$v=iR$

I think I managed to solve the entire problem, as I show below. My main doubt is about item (e), the incremental circuit.

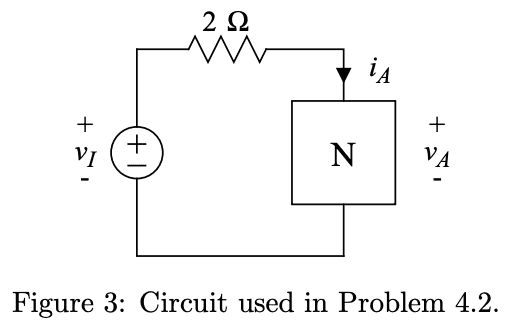
Part (a)

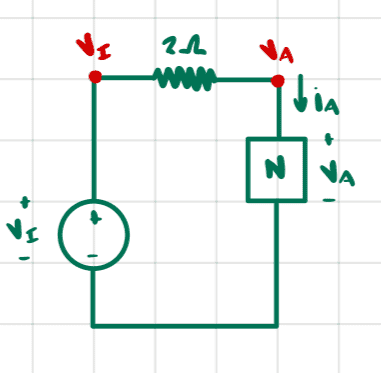
Using the node method and KCL we reach

$$\frac{v_I-v_A}{2}=10(1-e^{-v_A/5})\tag{1}$$

Part (b)
We can simplify (1) to

$$v_A=5\ln{\left ( \frac{20}{v_A+20-v_I} \right )}\tag{2}$$

If we sub in $v_I=\mathrm{10V}$ and use Newton-Raphson we find that $v_A=\mathrm{2.39V}$.

Part (c)
Now let $v_I=\mathrm{10.20V}$. Again by Newton-Raphson we find that $v_A=\mathrm{2.45V}$.

Thus, $\frac{\Delta v_A}{\Delta v_I}=\frac{0.06}{0.2}=0.3$.

Part (d)
Given $i_A=10(1-e^{v_A/5})$, linearization about $v_A=2.39\mathrm{V}$ gives us

$$\Delta i_A=2e^{-2.39/5}\Delta v_A\tag{3}$$

Note that this means that the incremental resistance of the nonlinear element is $\frac{1}{2e^{-2.39/5}}$.

Part (e)
I think the circuit is

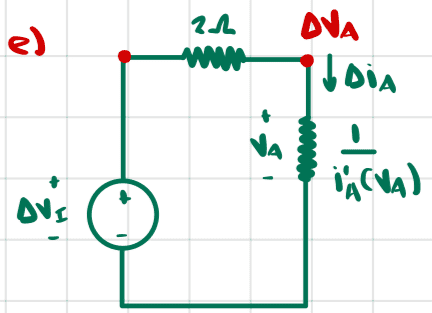
Part (f)
Using the node method and our linearized expression for $\Delta i_A$ we have

$$\frac{\Delta v_I-\Delta v_A}{2}=2e^{-2.39/5}\Delta v_A\tag{4}$$

For $\Delta v_I=0.2$ and solving for $\Delta v_A$ we get $\Delta v_A=0.0574$.

Thus, $\frac{\Delta v_A}{\Delta v_I}=\frac{0.0574}{0.2}\approx 0.287$.

We compare this with the value we found in (c) which was 0.3.

 

[TSny]

I think your work is correct.

For part (d) you might evaluate $2e^{-2.39/5}$ as a single number for the linear relation $\Delta i_A=2e^{-2.39/5}\Delta v_A$. Likewise, express the answer for the incremental resistance $\frac{1}{2e^{-2.39/5}}$ as a single numer with units.

In the diagram for part (e), you could indicate the resistance $\large \frac 1 {i'(v_A)}$ as a number with units.