- #1
zenterix
- 480
- 70
- TL;DR Summary
- While studying the book "Foundations of Analog and Digital Electronic Circuits" by Agarwal, I ran into an example that seems incorrect. I'd like to confirm that it is incorrect. I also include a small section about using the associated variables convention. The use of this convention sometimes confuses me, and I prefer to use a way that involves writing more things but avoids having to remember conventions.
Consider the following circuit
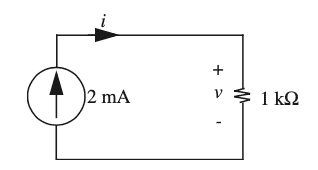
In Example 2.14 of Agarwal's "Foundations of Analog and Digital Electronic Circuits", he asks us to determine the value of v using energy conservation.
The result in the book is ##v=0.5\text{V}##. This seems incorrect according to my calculations.
I am learning about circuits, so even though I imagine this is a very simple example for some, I am trying to understand the concepts fully. Therefore, I will try to find the result in multiple ways.
The easiest path is to notice that ##i=2\text{mA}##. Then, by Ohm's law on the resistor we have
$$v=v^+-v^-=iR=2\text{mA}\times 1\mathrm{k\Omega}=2V\tag{1}$$
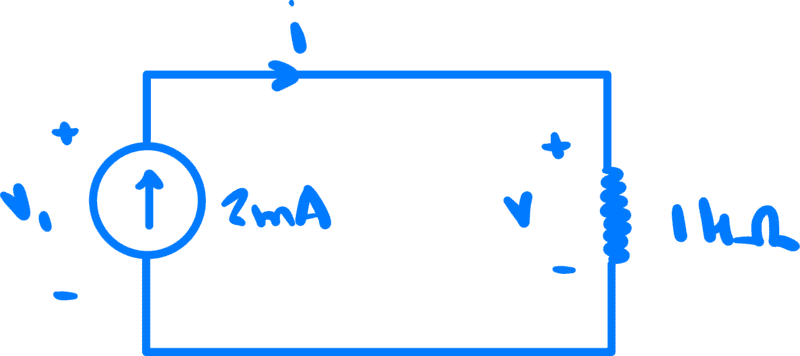
Next, I tried to obtain the same result using energy conservation
I prefer to write out the precise voltages I am subtracting based on conceptual knowledge instead of trying to memorize conventions because the latter confuse me.
The sum of the line integral of the electric field along a closed path is zero. This line integral on a counterclockwise path for the circuit above equals
$$(v_1^+-v_1^-)+(v^--v^+)=0\tag{2}$$
If we multiply both sides by ##i##, we get
$$i(v_1^+-v_1^-)+i(v^--v^+)=0\tag{3}$$
where the first term is power generated by the current source and the second term is power generated dissipated by the resistor (since this term comes out to be negative, we can call it power dissipated by the resistor).
Note that using (3), I believe the signs I am using are the opposite of what comes out when we use the associated variables convention (more on this in the last section of this post).
In this simple example we have only one loop so this multiplication isn't very useful for us.
We need only use (2), which gets us back to Ohm's law.
$$v_1^+-v_1^-=v^+-v^-=iR=2\text{mA}\times 1\mathrm{k\Omega}=2\text{V}\tag{4}$$
Note that the way I defined things, "power through the current source" is
$$2\text{mA}\times 2\text{V}=4\cdot 10^{-3}W$$
This comes from a current of ##2\cdot 10^{-3}\text{\frac{C}{s}}## going from a lower to a higher potential, where the latter difference is ##2\text{V}##, ie ##2\mathrm{\frac{J}{C}}##, resulting in each Coulomb of charge gaining ##4\cdot 10^{-3}\text{J}## of electric potential energy.
Similarly, we have the same current going from higher to lower potential through the resistor. A Coulomb of charge loses ##4\cdot 10^{-3}\text{J}## of electric potential energy.
This makes sense to me. Is it correct?
Assuming the above is correct, let me talk a little about why I find using the "associated variables convention" confusing in this problem.
This convention would have us do something as follows
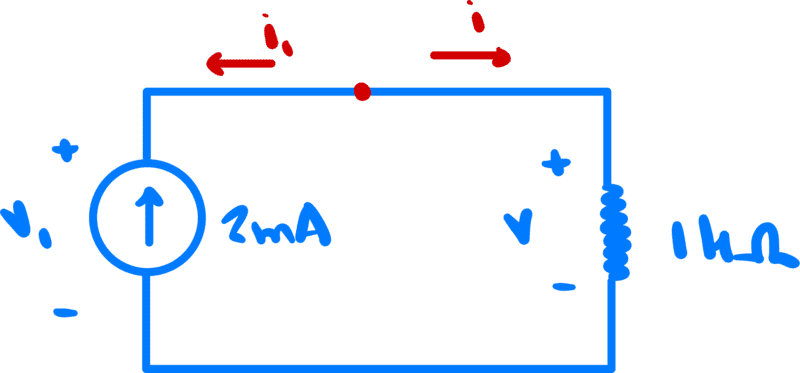
We define + and - terminals on each circuit element, define a terminal voltage for each circuit element as as the voltage on the + terminal minus the voltage on the - terminal, and we define a terminal current on each circuit element as entering through the + terminal on that element.
Then, KCL tells us
$$-i_1-i=0 \implies i_1=-i$$
We know that the current source generates ##2\text{mA}## moving in the opposite direction to ##i_1##, so ##i_1=-2\text{mA}##.
Hence,
$$i_1=-2\text{mA}=-i$$
$$i=2\text{mA}$$
The way I think about KVL, I write
$$(v_1^+-v_1^-)+(v^--v^+)=0$$
This is just
$$-v_1+v=0$$
Power into the current source is
$$i_1\times v_1=-2\text{mA}\times v_1$$
Similarly, power into the resistor is
$$i\times (v^+-v^-) = i\times v= i\times (iR)=i^2\times R = 2\text{mA}^2\times 1\mathrm{k\Omega}=4*10^{-3}\mathrm{W}$$
The part that I find confusing is the next step.
I guess the next step is to write that the sum of the power into the current source and the power into the resistor is zero.
$$i_1v_1+iv=0\tag{5}$$
$$-2\mathrm{mA}v_1+4*10^{-3}\mathrm{W}=-0$$
which we can solve for $v_1$
$$v_1=2V$$
Notice that the power into the resistor came out positive and the power into the current source came out negative.
I am struggling to understand what, for example, the following expression (power into the current source using the convention) tells us intuitively
$$i_1\cdot (v_1^+-v_1^-)\tag{6}$$
The way we've defined ##i_1## and ##v_1=v_1^+-v_1^-##, we have a current flowing from a higher to a lower potential. We know that this current is negative, so we can think of it as negative charges flowing.
However, when one Coulomb of negative charge flows through the current source, this charge gains ##v^--v^+## of electric potential energy.
On the other hand if we rewrite (6) as
$$(-i_1)\cdot (v_1^--v_1^+)\tag{6}$$
Then, we can interpret this as a positive current ##-i_1## flowing from a higher to a lower potential, and in this case what happens is that the change in energy for each Coulomb of positive charge is ##v^--v^+<0##. That is, the positive charge loses electric potential energy.
Somehow, we link this reasoning with the statement that the current source in question is generating power.
In Example 2.14 of Agarwal's "Foundations of Analog and Digital Electronic Circuits", he asks us to determine the value of v using energy conservation.
The result in the book is ##v=0.5\text{V}##. This seems incorrect according to my calculations.
I am learning about circuits, so even though I imagine this is a very simple example for some, I am trying to understand the concepts fully. Therefore, I will try to find the result in multiple ways.
The easiest path is to notice that ##i=2\text{mA}##. Then, by Ohm's law on the resistor we have
$$v=v^+-v^-=iR=2\text{mA}\times 1\mathrm{k\Omega}=2V\tag{1}$$
Next, I tried to obtain the same result using energy conservation
I prefer to write out the precise voltages I am subtracting based on conceptual knowledge instead of trying to memorize conventions because the latter confuse me.
The sum of the line integral of the electric field along a closed path is zero. This line integral on a counterclockwise path for the circuit above equals
$$(v_1^+-v_1^-)+(v^--v^+)=0\tag{2}$$
If we multiply both sides by ##i##, we get
$$i(v_1^+-v_1^-)+i(v^--v^+)=0\tag{3}$$
where the first term is power generated by the current source and the second term is power generated dissipated by the resistor (since this term comes out to be negative, we can call it power dissipated by the resistor).
Note that using (3), I believe the signs I am using are the opposite of what comes out when we use the associated variables convention (more on this in the last section of this post).
In this simple example we have only one loop so this multiplication isn't very useful for us.
We need only use (2), which gets us back to Ohm's law.
$$v_1^+-v_1^-=v^+-v^-=iR=2\text{mA}\times 1\mathrm{k\Omega}=2\text{V}\tag{4}$$
Note that the way I defined things, "power through the current source" is
$$2\text{mA}\times 2\text{V}=4\cdot 10^{-3}W$$
This comes from a current of ##2\cdot 10^{-3}\text{\frac{C}{s}}## going from a lower to a higher potential, where the latter difference is ##2\text{V}##, ie ##2\mathrm{\frac{J}{C}}##, resulting in each Coulomb of charge gaining ##4\cdot 10^{-3}\text{J}## of electric potential energy.
Similarly, we have the same current going from higher to lower potential through the resistor. A Coulomb of charge loses ##4\cdot 10^{-3}\text{J}## of electric potential energy.
This makes sense to me. Is it correct?
Assuming the above is correct, let me talk a little about why I find using the "associated variables convention" confusing in this problem.
This convention would have us do something as follows
We define + and - terminals on each circuit element, define a terminal voltage for each circuit element as as the voltage on the + terminal minus the voltage on the - terminal, and we define a terminal current on each circuit element as entering through the + terminal on that element.
Then, KCL tells us
$$-i_1-i=0 \implies i_1=-i$$
We know that the current source generates ##2\text{mA}## moving in the opposite direction to ##i_1##, so ##i_1=-2\text{mA}##.
Hence,
$$i_1=-2\text{mA}=-i$$
$$i=2\text{mA}$$
The way I think about KVL, I write
$$(v_1^+-v_1^-)+(v^--v^+)=0$$
This is just
$$-v_1+v=0$$
Power into the current source is
$$i_1\times v_1=-2\text{mA}\times v_1$$
Similarly, power into the resistor is
$$i\times (v^+-v^-) = i\times v= i\times (iR)=i^2\times R = 2\text{mA}^2\times 1\mathrm{k\Omega}=4*10^{-3}\mathrm{W}$$
The part that I find confusing is the next step.
I guess the next step is to write that the sum of the power into the current source and the power into the resistor is zero.
$$i_1v_1+iv=0\tag{5}$$
$$-2\mathrm{mA}v_1+4*10^{-3}\mathrm{W}=-0$$
which we can solve for $v_1$
$$v_1=2V$$
Notice that the power into the resistor came out positive and the power into the current source came out negative.
I am struggling to understand what, for example, the following expression (power into the current source using the convention) tells us intuitively
$$i_1\cdot (v_1^+-v_1^-)\tag{6}$$
The way we've defined ##i_1## and ##v_1=v_1^+-v_1^-##, we have a current flowing from a higher to a lower potential. We know that this current is negative, so we can think of it as negative charges flowing.
However, when one Coulomb of negative charge flows through the current source, this charge gains ##v^--v^+## of electric potential energy.
On the other hand if we rewrite (6) as
$$(-i_1)\cdot (v_1^--v_1^+)\tag{6}$$
Then, we can interpret this as a positive current ##-i_1## flowing from a higher to a lower potential, and in this case what happens is that the change in energy for each Coulomb of positive charge is ##v^--v^+<0##. That is, the positive charge loses electric potential energy.
Somehow, we link this reasoning with the statement that the current source in question is generating power.
Last edited: