MHB Log Integral: $\displaystyle \frac{\pi^2}{b^2} \csc^2\left(\frac{\pi}{b}\right)$

[polygamma]

Show that for $ \displaystyle b>1, \ \int_{0}^{\infty} \frac{\ln x}{x^{b}-1} \ dx = \frac{\pi^{2}}{b^{2}} \csc^{2} \left(\frac{\pi}{b} \right)$.

 

[chisigma]

Re: a "simple" log integral

Show that for $ \displaystyle b>1, \ \int_{0}^{\infty} \frac{\ln x}{x^{b}-1} \ dx = \frac{\pi^{2}}{b^{2}} \csc^{2} \left(\frac{\pi}{b} \right)$.

With the substitution $b\ \ln x = t$ the integral becomes...

$\displaystyle \frac{1}{b^{2}}\ \int_{- \infty}^{+ \infty} \frac{t}{e^{t}-1}\ e^{\frac{t}{b}}\ dt\ (1)$ ... and the (1) can be attacked with the residue theorem or Fourier Transform technique...

Kind regards

$\chi$ $\sigma$

 

[alyafey22]

Re: "simple" log integral

I will confess that kook me a while to figure out I was looking for a real method but failed horribly (Angry)

Consider the following function

$$f(z) = \frac{\log(z)}{e^{b\log(z)}-1}$$

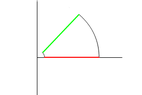
Now consider a sector with an angle of $\frac{\pi}{b}$

View attachment 1095

The integration of the whole sector is $0$ since the function is analytic in and on the contour by taking the principle branch of the logarithm .The integration along the x-axis is

$$\int^{R}_{r} \frac{\log(x)}{x^b-1}$$

The integration along the big and small circular sectors

It can be proven easily by taking $$r\to 0 , R \to \infty$$ that they vanish.

The integration along the tilted line

can be viewed using the transformation $z=te^{i\frac{\pi}{b}}$ , $R<t<r$

$$-e^{\frac{\pi i}{b}}\int^{R}_r \frac{\log(te^{\frac{\pi i}{b}})}{e^{b\log\left(\frac{\pi i}{b} \right)}-1}\, dt$$

$$e^{\frac{\pi i}{b}}\int^{R}_r \frac{\log(t)+i\frac{\pi}{b}}{t^b+1}\, dt$$

$$e^{\frac{\pi i}{b}}\int^{R}_r \frac{\log(t)}{t^b+1}\, dt+ie^{\frac{\pi i}{b}}\int^{R}_0\frac{\frac{\pi}{b}}{t^b+1}\, dt\,\,\, (1)$$

The integrals can be easily found using the beta function by taking the principle value and
$$r\to 0 \,\,\,\, , \,\,\,\, R \to \infty$$

$$e^{\frac{\pi i}{b}} \left( -\frac{\pi^2}{b^2} \csc\left( \frac{\pi}{b}\right) \cot\left( \frac{\pi}{b}\right)+i\frac{\pi^2}{b^2} \csc\left( \frac{\pi}{b}\right)\right)$$

This can be written as $$-\frac{\pi^2e^{\frac{\pi i}{b}}}{b^2} \csc\left( \frac{\pi}{b}\right) \left( \cot\left( \frac{\pi}{b}\right)-i\right)$$

$$-\frac{\pi^2e^{\frac{\pi i}{b}}}{b^2} \csc^2\left( \frac{\pi}{b}\right) \left( \cos\left( \frac{\pi}{b}\right)-i\sin\left( \frac{\pi}{b}\right)\right)$$

Now using the Euler formula we have

$$-\frac{\pi^2}{b^2} \csc^2\left( \frac{\pi}{b}\right)$$

Summing the curves together and using Cauchy integral formula gives the desired result .

Note : If someone is interested on the evaluations of (1) , I can show them .

 

[alyafey22]

Re: "simple" log integral

EDIT :

We have to find the zeros of the equation $$z^b = 1$$ for $$b>1$$ then we have

$$z = e^{\frac{ 2 \pi }{b}i }$$

According to W|A the residue is equal to $0$ , but we have to prove it .

 

[polygamma]

Re: "simple" log integral

Another approach using contour integration is to evaluate $ \displaystyle \text{PV} \int_{0}^{\infty} \frac{x^{a-1}}{x^{b}-1} \ dx$ and then differentiate inside of the integral.Let $ \displaystyle f(z) = \frac{z^{a-1}}{z^{b}-1}$ and integrate around a wedge of radius $R$ that makes an angle of $ \displaystyle \frac{2 \pi}{b}$ with the positive real axis and is indented at $z=0, z=1$, and $ \displaystyle z = e^{\frac{2 \pi i}{b}}$.

Then $ \displaystyle \text{PV} \int_{0}^{\infty} f(z) \ dz - \pi i \text{Res} [f,1]+ \lim_{R \to \infty} \int_{0}^{\frac{2 \pi}{b}} f(Re^{it}) iRe^{it} \ dt - \pi i \int_{0}^{\infty} f(te^{\frac{2 \pi i }{b}}) e^{\frac{2 \pi i}{b}} \ dt $

$ - \displaystyle \pi i \text{Res}[f,e^{\frac{2 \pi i}{b}}] - \lim_{r \to 0} \int_{0}^{\frac{2 \pi}{b}} f(re^{it}) ire^{it} \ dt = 0$$ \displaystyle \text{Res}[f,1] = \lim_{z \to 1} \frac{z^{a-1}}{bz^{b-1}} = \frac{1}{b}$$ \displaystyle \Big| \int_{0}^{\frac{2 \pi}{b}} f(Re^{it}) iRe^{it} \ dt \Big| \le \int_{0}^{\frac{2 \pi}{b}} \Big|\frac{R^{a-1} e^{it(a-1)}}{R^{b}e^{itb}-1} i Re^{it} \Big| dt \le \frac{2 \pi}{b} \frac{R^{a}}{R^{b}-1} \to 0$ as $R \to \infty$$ \displaystyle \int_{0}^{\infty} f(te^{\frac{2 \pi i }{b}}) e^{\frac{2 \pi i}{b}} \ dt = e^{\frac{2 \pi i}{b}} \int_{0}^{\infty} \frac{t^{a-1} e^{\frac{2 \pi i(a-1)}{b}}}{t^{b} e^{2 \pi i} - 1} \ dt = e^{\frac{2 \pi i}{b}} e^{\frac{2 \pi i(a-1)}{b}} \text{PV} \int_{0}^{\infty} \frac{t^{a-1}}{t^{b}-1} \ dt$$\displaystyle \text{Res}[f, e^{\frac{2 \pi i}{b}}] = \lim_{z \to e^{\frac{2 \pi i}{b}}} \frac{z^{a-1}}{bz^{b-1}} = \frac{e^{\frac{2 \pi i (a-1)}{b}}}{b e^{\frac{2 \pi i(b-1)}{b}}} = \frac{1}{b} e^{\frac{2 \pi i}{b}} e^{\frac{2 \pi i (a-1)}{b}}$$ \displaystyle \Big| \int_{0}^{\frac{2 \pi}{b}} f(re^{it}) ire^{it} \ dt \Big| \le \frac{2 \pi}{b} \frac{r^{a}}{1-r^{b}} \to 0$ as $r \to 0$So $ \displaystyle \text{PV} \int_{0}^{\infty} \frac{x^{a-1}}{x^{b}-1} \ dx - \frac{\pi i}{b} - e^{\frac{2 \pi i}{b}} e^{\frac{2 \pi i(a-1)}{b}} \text{PV} \int_{0}^{\infty} \frac{t^{a-1}}{t^{b}-1} \ dt - \frac{\pi i}{b} e^{\frac{2 \pi i}{b}} e^{\frac{2 \pi i (a-1)}{b}} = 0$

$ \displaystyle \implies \text{PV} \int_{0}^{\infty} \frac{x^{a-1}}{x^{b}-1} \ dx = \frac{\pi i}{b} \frac{1 + e^{\frac{2 \pi i}{b}} e^{\frac{2 \pi i (a-1)}{b}}}{1-e^{\frac{2 \pi i}{b}} e^{\frac{2 \pi i (a-1)}{b}}} = \frac{\pi i}{b} \frac{1 + e^{\frac{2 \pi i a}{b}}}{1-e^{\frac{2 \pi i a}{b}}} = - \frac{\pi}{b} \cot \left(\frac{\pi a}{b} \right)$Then $ \displaystyle \int_{0}^{\infty} \frac{x^{a-1} \ln x}{x^{b}-1} \ dx = - \frac{\partial}{\partial a} \frac{\pi}{b} \cot \left(\frac{\pi a}{b} \right) = \frac{\pi^{2}}{b^{2}} \csc^{2} \left(\frac{\pi a}{b} \right)$And $ \displaystyle \int_{0}^{\infty} \frac{\ln x}{x^{b} - 1} \ dx = \frac{\pi^{2}}{b^{2}} \csc^{2} \left(\frac{\pi}{b} \right)$

 

[polygamma]

Re: "simple" log integral

I have to do some adjustments , I thought the pole is at $z=-1$ , but actually there is another at $z=1$ so we have to indent at $z=1$ and evaluate again

$\displaystyle \frac{\log z}{z^{b}-1}$ does not have a pole at $z=1$ but rather a removable singularity

 

[alyafey22]

Re: "simple" log integral

$\displaystyle \frac{\log z}{z^{b}-1}$ does not have a pole at $z=1$ but rather a removable singularity

Yup I wasn't thinking properly ..

$$\lim_{z \to 1}\frac{\log(z)}{z^b -1}=\frac{1}{b}$$

It remains the poles at the point $e^{\frac{2\pi }{b} i }$ , since the function is not multivalued , we are going only once around the circle .

It should lie out side the contour !

 

[alyafey22]

Re: "simple" log integral

Seems you have taken a completely different approach , I was thinking completely different .

Have you thought of real methods ?