Firepanda
- 425
- 0
I have to do the following using these axioms PA1-7, the others below it are previously proved results I can use too.
[Sa] means the successor of a.
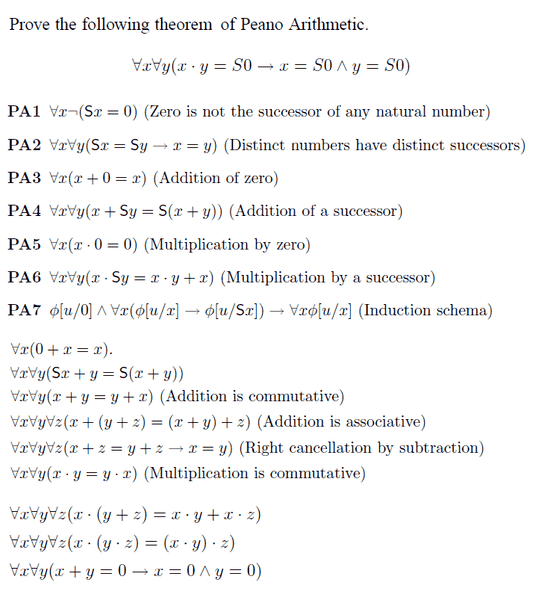 Base Case: y = S0
Base Case: y = S0
x.S0 = S0
→ x.0 + x = S0
→ 0 + x = S0
→ x = S0 & y=S0
Now the induction step is usually y=a to y=Sa, however this does not work here, I assume I need to take a new y and it's successor to proceed. Would anyone know how to proceed and which y to take?
Thanks
[Sa] means the successor of a.
x.S0 = S0
→ x.0 + x = S0
→ 0 + x = S0
→ x = S0 & y=S0
Now the induction step is usually y=a to y=Sa, however this does not work here, I assume I need to take a new y and it's successor to proceed. Would anyone know how to proceed and which y to take?
Thanks