Other papers by people other than the authors of this paper and Deur pursuing the same basic agenda of explaining Dark Matter phenomena with unmodified General Relativity rather than a Newtonian approximation include the following (nine of which date to 2018 or later, reflecting a recent surge of activity in this research agenda):
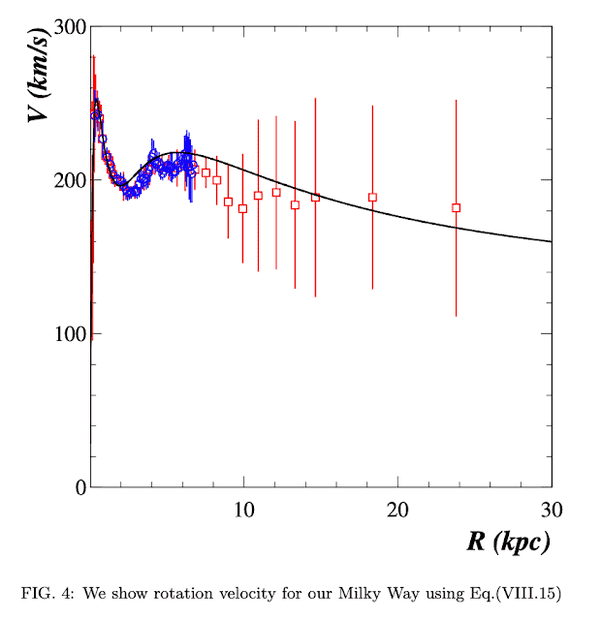
Historically, the existence of dark matter has been postulated to resolve discrepancies between astrophysical observations and accepted theories of gravity. In particular, the measured rotation curve of galaxies provided much experimental support to the dark matter concept. However, most theories used to explain the rotation curve have been restricted to the Newtonian potential framework, disregarding the general relativistic corrections associated with mass currents. In this paper it is shown that the gravitomagnetic field produced by the currents modifies the galactic rotation curve, notably at large distances. The coupling between the Newtonian potential and the gravitomagnetic flux function results in a nonlinear differential equation that relates the rotation velocity to the mass density. The solution of this equation reproduces the galactic rotation curve without recourse to obscure dark matter components, as exemplified by three characteristic cases. A bi-dimensional model is developed that allows to estimate the total mass, the central mass density, and the overall shape of the galaxies, while fitting the measured luminosity and rotation curves. The effects attributed to dark matter can be simply explained by the gravitomagnetic field produced by the mass currents.
G. O. Ludwig, "
Galactic rotation curve and dark matter according to gravitomagnetism" 81 The European Physical Journal C 186 (February 23, 2021) (open access).
We consider the consequences of applying general relativity to the description of the dynamics of a galaxy, given the observed flattened rotation curves. The galaxy is modeled as a stationary axially symmetric pressure-free fluid. In spite of the weak gravitational field and the non-relativistic source velocities, the mathematical system is still seen to be non-linear. It is shown that the rotation curves for various galaxies as examples are consistent with the mass density distributions of the visible matter within essentially flattened disks. This obviates the need for a massive halo of exotic dark matter. We determine that the mass density for the luminous threshold as tracked in the radial direction is 10^−21.75 kg⋅m^−3 for these galaxies and conjecture that this will be the case for other galaxies yet to be analyzed. We present a velocity dispersion test to determine the extent, if of any significance, of matter that may lie beyond the visible/HI region. Various comments and criticisms from colleagues are addressed.
F.I. Cooperstock, S. Tieu, "
Galactic dynamics via general relativity: a compilation and new developments." 22 Int. J. Mod. Phys. A 2293–2325 (2007).
arXiv:astro-ph/0610370 See also follow up papers in
2007, in
2011, and
2015.
Exact stationary axially symmetric solutions to the four-dimensional Einstein equations with corotating pressureless perfect fluid sources are studied. A particular solution with an approximately flat rotation curve is discussed in some detail. We find that simple Newtonian arguments overestimate the amount of matter needed to explain such curves by more than 30%. The crucial insight gained by this model is that the Newtonian approximation breaks down in an extended rotating region, even though it is valid locally everywhere. No conflict with solar system tests arises.
H. Balasin, D. Grumiller, "
Non-Newtonian behavior in weak field general relativity for extended rotating sources." 17 Int. J. Mod. Phys. D 475–488 (2008) (arXiv version
here).
Flat rotation curves (RCs) in disc galaxies provide the main observational support to the hypothesis of surrounding dark matter (DM). Despite of the difficulty in identifying the DM contribution to the total mass density in our Galaxy, stellar kinematics, as tracer of gravitational potential, is the most reliable observable for gauging different matter components. From the Gaia second data release catalogue, we extracted parallaxes, proper motions, and line-of-sight velocities of unprecedented accuracy for a carefully selected sample of disc stars. This is the angular momentum supported population of the Milky Way (MW) that better traces its observed RC.
We fitted such data to both a classical, i.e. including a DM halo, velocity profile model, and a general relativistic one derived from a stationary axisymmetric galaxy-scale metric. The general relativistic MW RC results statistically indistinguishable from its state-of-the-art DM analogue. This supports the ansatz that a weak gravitational contribution due to the off-diagonal term of the metric, by explaining the observed flatness of MW’s RC, could fill the gap in a baryons-only MW, thus rendering the Newtonian-origin DM a general relativity-like effect. In the context of Local Cosmology, our findings are suggestive of the Galaxy’s phase space as the exterior gravitational field in equilibrium far from a Kerr-like inner source, possibly with no need for extra matter to account for the disc kinematics.
M. Crosta, M. Giammaria, M.G. Lattanzi, E. Poggio, "
On testing CDM and geometry-driven Milky Way rotation curve models with Gaia DR2." 496 Mon. Not. R. Astron. Soc. 2107–2122 (2020) (open access).
In Newtonian gravity, mass is an intrinsic property of matter while in general relativity (GR), mass is a contextual property of matter, i.e., matter can simultaneously possesses two different values of mass when it is responsible for two different spatiotemporal geometries. Herein, we explore the possibility that the astrophysical missing mass attributed to non-baryonic dark matter (DM) actually obtains because we have been assuming the Newtonian view of mass rather than the GR view. Since an exact GR solution for realistic astrophysical situations is not feasible, we explore GR-motivated ansatzes relating proper mass and dynamic mass for one and the same baryonic matter, as justified by GR contextuality. We consider four GR alternatives and find that the GR ansatz motivated by metric perturbation theory works well in fitting galactic rotation curves (THINGS data), the mass profiles of X-ray clusters (ROSAT and ASCA data) and the angular power spectrum of the cosmic microwave background (CMB, Planck 2015 data) without DM. We compare our galactic rotation curve fits to modified Newtonian dynamics (MOND), Burkett halo DM and Navarro-Frenk-White (NFW) halo DM. We compare our X-ray cluster mass profile fits to metric skew-tensor gravity (MSTG) and core-modified NFW DM. We compare our CMB angular power spectrum fit to scalar-tensor-vector gravity (STVG) and ΛCDM. Overall, we find our fits to be comparable to those of MOND, MSTG, STVG, ΛCDM, Burkett, and NFW. We present and discuss correlations and trends for the best fit values of our fitting parameters. For the most part, the correlations are consistent with well-established results at all scales, which is perhaps surprising given the simple functional form of the GR ansatz.
W.M. Stuckey, Timothy McDevitt, A.K. Sten, Michael Silberstein, "
The Missing Mass Problem as a Manifestation of GR Contextuality" 27(14) International Journal of Modern Physics D 1847018 (2018). DOI: 10.1142/S0218271818470181.
We push ahead the idea developed in [24], that some fraction of the dark matter and the dark energy can be explained as a relativistic effect. The inhomogeneity matter generates gravitational distortions, which are general relativistically retarded. These combine in a magnification effect since the past matter density, which generated the distortion we feel now, is greater than the present one. The non negligible effect on the averaged expansion of the universe contributes both to the estimations of the dark matter and to the dark energy, so that the parameters of the Cosmological Standard Model need some corrections.
In this second work we apply the previously developed framework to relativistic models of the universe. It results that one parameter remain free, so that more solutions are possible, as function of inhomogeneity. One of these fully explains the dark energy, but requires more dark matter than the Cosmological Standard Model (91% of the total matter). Another solution fully explains the dark matter, but requires more dark energy than the Cosmological Standard Model (15% more). A third noteworthy solution explains a consistent part of the dark matter (it would be 63% of the total matter) and also some of the dark energy (4%).
Federico Re, "
Fake dark matter from retarded distortions" (May 30, 2020).
We show that Einstein's conformal gravity is able to explain simply on the geometric ground the galactic rotation curves without need to introduce any modification in both the gravitational as well as in the matter sector of the theory.
The geometry of each galaxy is described by a metric obtained making a singular rescaling of the Schwarzschild's spacetime. The new exact solution, which is asymptotically Anti-de Sitter, manifests an unattainable singularity at infinity that can not be reached in finite proper time, namely, the spacetime is geodetically complete. It deserves to be notice that we here think different from the usual. Indeed, instead of making the metric singularity-free, we make it apparently but harmlessly even more singular then the Schwarzschild's one.
Finally, it is crucial to point that the Weyl's conformal symmetry is spontaneously broken to the new singular vacuum rather then the asymptotically flat Schwarzschild's one. The metric, is unique according to: the null energy condition, the zero acceleration for photons in the Newtonian regime, and the homogeneity of the Universe at large scales.
Once the matter is conformally coupled to gravity, the orbital velocity for a probe star in the galaxy turns out to be asymptotically constant consistently with the observations and the Tully-Fisher relation. Therefore, we compare our model with a sample of 175 galaxies and we show that our velocity profile very well interpolates the galactic rotation-curves for a proper choice of the only free parameter in the metric and the the mass to luminosity ratios, which turn out to be close to 1 consistently with the absence of dark matter.
Leonardo Modesto, Tian Zhou, Qiang Li, "Geometric origin of the galaxies' dark side"
arXiv:2112.04116 (December 8, 2021).
The metric tensor in the four dimensional flat space-time is represented as the matrix form and then the transformation is performed for successive Lorentz boost. After extending or more generalizations the transformation of metric is derived for the curved space-time, manifested after the synergy of different sources of mass. The transformed metric in linear perturbation interestingly reveals a shift from Newtonian gravity for two or more than two body system.
Shubhen Biswas, "The metric transformations and modified Newtonian gravity"
arXiv:2109.13515 (September 28, 2021) (note that this not a "MOND" paper, as used in the title "modified Newtonian gravity" means Newtonian gravity with GR based adjustments).
The flattening of spiral-galaxy rotation curves is unnatural in view of the expectations from Kepler's third law and a central mass. It is interesting, however, that the radius-independence velocity is what one expects in one less dimension. In our three-dimensional space, the rotation curve is natural if, outside the galaxy's center, the gravitational potential corresponds to that of a very prolate ellipsoid, filament, string, or otherwise cylindrical structure perpendicular to the galactic plane. While there is observational evidence (and numerical simulations) for filamentary structure at large scales, this has not been discussed at scales commensurable with galactic sizes. If, nevertheless, the hypothesis is tentatively adopted, the scaling exponent of the baryonic Tully--Fisher relation due to accretion of visible matter by the halo comes out to reasonably be 4. At a minimum, this analytical limit would suggest that simulations yielding prolate haloes would provide a better overall fit to small-scale galaxy data.
Felipe J. Llanes-Estrada, "
Elongated Gravity Sources as an Analytical Limit for Flat Galaxy Rotation Curves" 7(9) Universe 346
arXiv:2109.08505 (September 16, 2021) DOI:
10.3390/universe7090346
Inspired by the statistical mechanics of an ensemble of interacting particles (BBGKY hierarchy), we propose to account for small-scale inhomogeneities in self-gravitating astrophysical fluids by deriving a non-ideal Virial theorem and non-ideal NavierStokes equations. These equations involve the pair radial distribution function (similar to the two-point correlation function used to characterize the large-scale structures of the Universe), similarly to the interaction energy and equation of state in liquids. Within this framework, small-scale correlations lead to a non-ideal amplification of the gravitational interaction energy, whose omission leads to a missing mass problem, e.g., in galaxies and galaxy clusters.
We propose to use a decomposition of the gravitational potential into a near- and far-field component in order to account for the gravitational force and correlations in the thermodynamics properties of the fluid. Based on the non-ideal Virial theorem, we also propose an extension of the Friedmann equations in the non-ideal regime and use numerical simulations to constrain the contribution of these correlations to the expansion and acceleration of the Universe.
We estimate the non-ideal amplification factor of the gravitational interaction energy of the baryons to lie between 5 and 20, potentially explaining the observed value of the Hubble parameter (since the uncorrelated energy account for ∼ 5%). Within this framework, the acceleration of the expansion emerges naturally because of the increasing number of sub-structures induced by gravitational collapse, which increases their contribution to the total gravitational energy. A simple estimate predicts a non-ideal deceleration parameter qni ' -1; this is potentially the first determination of the observed value based on an intuitively physical argument. We show that another consequence of the small-scale gravitational interactions in bound structures (spiral arms or local clustering) yields a transition to a viscous regime that can lead to flat rotation curves. This transition can also explain the dichotomy between (Keplerian) LSB elliptical galaxy and (non-Keplerian) spiral galaxy rotation profiles. Overall, our results demonstrate that non-ideal effects induced by inhomogeneities must be taken into account, potentially with our formalism, in order to properly determine the gravitational dynamics of galaxies and the larger scale universe.
P. Tremblin, et al., "
Non-ideal self-gravity and cosmology: the importance of correlations in the dynamics of the large-scale structures of the Universe" arXiv:2109.09087 (September 19, 2021) (submitted to A&A, original version submitted in 2019).
Honorable mention goes to Lorenzo Posti, S. Michael Fall "
Dynamical evidence for a morphology-dependent relation between the stellar and halo masses of galaxies" Accepted for publication in A&A.
arXiv:2102.11282 [astro-ph.GA] (February 22, 2021) which notes the relationship at the center of Deur's framework which is the relationship between a system's shape and the dark matter phenomena which it exhibits.