Lyapunov Stability for a nonlinear system

[Arman777]

I am trying to understand attracting, Liapunov stable, asymptotically stable for given coupled system. I don't have any Liapunov function. Just two coupled systems such as

$\dot{x} = y$, $\dot{y} = -4x$

or sometimes normal systems

$\dot{x} = -x$, $\dot{y} = -5y$
How can I approach to this problem. Do I have to find the eigenvalues and then eigenvectors, write the solution etc or can it be determined just by looking at the eigenvalues ?

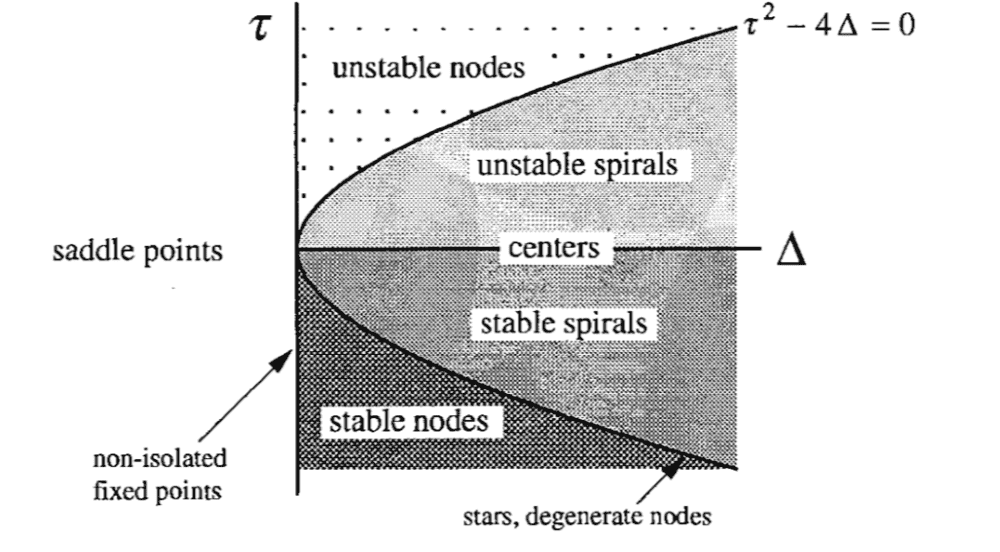
Or is it useful to use this diagram ?
[![enter image description here][1]][1]
I guess it can be determined from
$\lambda_{1,2} = \frac{1}{2} (\tau \pm \sqrt{\tau^2 - 4\Delta})$
$\tau = \lambda_1 + \lambda_2$ and $\Delta = \lambda_1 \lambda_2$

This is a new subject to me so I am kind of confused.

 

[S.G. Janssens]

The linear systems you write down are of the form $\dot{x}(t) = Ax(t)$ for some real, constant $n \times n$ matrix $A$. Given the title of this topic, I assume that these systems arise as linearizations (at a zero equilibrium, for simplicity) of nonlinear autonomous ODEs.

The basic theorem (sometimes known as the "principle of linearized stability") about this situation says that the local (in)stability of the original, nonlinear system can be inferred from the (in)stability of its linearization, provided that $A$ does not have spectrum (eigenvalues) on the imaginary axis.

In turn, a linear system of the form $\dot{x}(t) = Ax(t)$ is asymptotically stable if all eigenvalues have real parts strictly less than zero, and unstable if there is at least one eigenvalue with real part strictly greater than zero. If there are eigenvalues on the imaginary axis, then conclusions from the linear system do not (in general) carry over to the nonlinear system. (In this case, one may proceed to calculate a higher order "normal form".)

The diagram you show is for linear systems in the particular case $n = 2$. In this case, you can express the eigenvalue pair (and especially the real parts) in terms of the determinant $\Delta$ and trace $\tau$ of $A$. Some people find the $(\Delta,\tau)$-plane a useful aid for stability considerations, but I think it is often easier to consider the eigenvalues directly.