Magnetic Dipole Field from a Loop of Wire

[bcerge1]

I am trying to understand the magnetic dipole field via loop of wire.

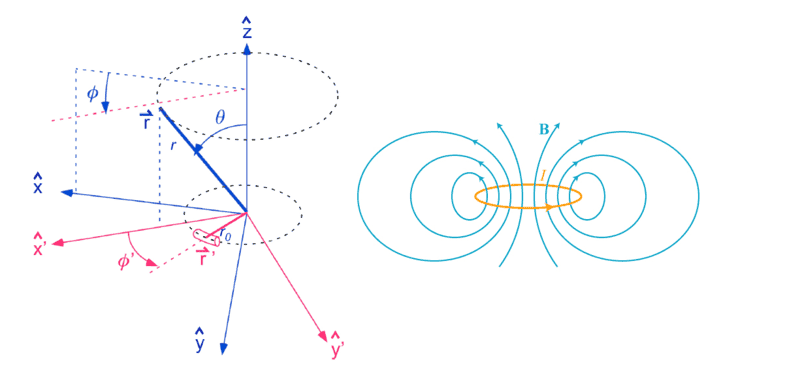
The above pictures show how this problem is typically setup and how the field lines are typically shown.
The math is messy but every textbook yields the following:

β = ∇xA = (m / (4⋅π⋅R³)) ⋅ (2⋅cos(θ) r + sin(θ) θ)

The issue I am having is seeing how the above equation yields the field lines from the above picture.
If θ is referenced from the Z axis, and the loop of wire is on the X-Y axis, in my mind the field lines are 90 degrees shifted. In other words, when θ=0, the radial component is at it's max straight up the Z-axis, and as θ approaches π/2 the radial component approaches 0. The above picture shows that β is max at π/2 and not 0. In Matlab I plotted a few different Radii for all θ = 0 to 2π and Φ=0:

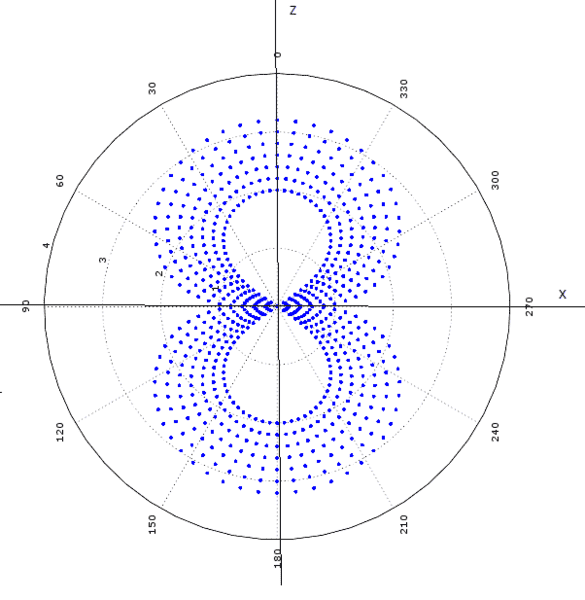
This picture is 90 degrees shifted from how I think it should be. Can someone help me understand this? Why does the equation not align up with the way the typical picture is shown? Am I incorrect in assuming the Z-axis is perpendicular to loop? Am i missing something? Am i not even close? D:

 

[BvU]

Hello bc,

I plotted a few different Radii

What are Radii ? If I connect the dots in one way, I get the field lines from the picture at the top right (*). Perpendicular to those are the lines of constant |B| .

(*) but that picture has a non-zero size loop, the picture you made is for an infinitesimally small loop.

 

[bcerge1]

If i understand the equation correctly, the magnitude of the equation is the m / (4⋅π⋅R³). the R is the distance from the wire to the point of the B field being measured. I suppose its not technically a 'radius', rather a distance. The plot i created was for 7 different R values for θ = 0 to 2π.

I think where I am going wrong is trying to visualize the field coming the origin (infinitesimally small point at (0,0,0)) and not from a point on the wire. In other words, i might need to model the equation to include the geometry of the loop?

 

[scottdave]

The strength of B is how tightly packed the magnetic flux lines are (density of the flux), rather than distance from the origin. So at pi/2, the lines are spaced far apart, while at 0 they are more dense.

 

[bcerge1]

So is plotting the magnetic field lines (upper right hand corner picture) different than plotting the B field?

 

[BvU]

Plotting the B field can be done two ways: follow the field lines (that's the usual way) or connect points with the same field strength.