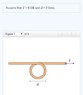
SUMMARY
The strength of the magnetic field at the center of a loop can be calculated using the formula B = Mu_0*I/(2*R). However, in this discussion, the scenario involves a loop combined with a straight wire, which complicates the application of this formula. The correct approach is to use the principle of superposition, adding the magnetic field contributions from both the loop and the straight wire. This method ensures accurate calculations for magnetic fields in complex configurations.
PREREQUISITES
- Understanding of magnetic field equations, specifically B = Mu_0*I/(2*R)
- Knowledge of superposition principle in electromagnetism
- Familiarity with the geometry of magnetic fields from loops and straight wires
- Basic concepts of current-carrying conductors
NEXT STEPS
- Study the principle of superposition in electromagnetism
- Learn about magnetic fields generated by straight wires
- Explore the effects of loop geometry on magnetic field strength
- Investigate applications of Ampère's Law in complex circuits
USEFUL FOR
Students and educators in physics, electrical engineers, and anyone interested in understanding magnetic fields in complex configurations involving loops and straight wires.