Badger
- 28
- 0
Hi, can someone help me out? I've tried 5 different solution that I thought were definitely right and they all give me the same response: "Your answer is off by a multiplicative factor."
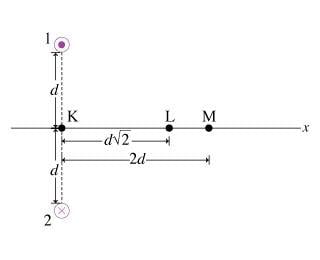
Find the magnitude of the net magnetic field B_L created at point L by both wires.
Express your answer in terms of I, d, and appropriate constants.
<br /> B_{\rm wire}=\frac{\mu_0 I}{2\pi d} ,<br />
The question before this: there was a question:
Point L is located a distance d\sqrt 2 from the midpoint between the two wires. Find the magnitude of the magnetic field B_1L created at point L by wire 1.I put in the answer and got it right.
<br /> B_1L =\left({\mu}_{0}I\right)/\left[2{\pi}\sqrt{\left(d^{2}+\left(d\sqrt{2}\right)^{2}\right)}\right]<br />
So for the question at hand, I put in the same equation and multiplied by 2, figuring the net force would be the 2 separate forces added, which are equal since they both give the same direction of magnetic force and to do the same degree.
It didn't work.
So maybe it works like a loop since the top current is coming out at distance d and the bottom current is going in at distance d. d is now a radius.
so I tried
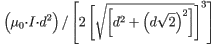
Also wrong. Tried to input it in various ways, ^(3/2), cancel out the pi's. Still wrong, "my answer is off by a multiplicative factor."
Help would be awesome!
Homework Statement
Find the magnitude of the net magnetic field B_L created at point L by both wires.
Express your answer in terms of I, d, and appropriate constants.
Homework Equations
<br /> B_{\rm wire}=\frac{\mu_0 I}{2\pi d} ,<br />
The Attempt at a Solution
The question before this: there was a question:
Point L is located a distance d\sqrt 2 from the midpoint between the two wires. Find the magnitude of the magnetic field B_1L created at point L by wire 1.I put in the answer and got it right.
<br /> B_1L =\left({\mu}_{0}I\right)/\left[2{\pi}\sqrt{\left(d^{2}+\left(d\sqrt{2}\right)^{2}\right)}\right]<br />
So for the question at hand, I put in the same equation and multiplied by 2, figuring the net force would be the 2 separate forces added, which are equal since they both give the same direction of magnetic force and to do the same degree.
It didn't work.
So maybe it works like a loop since the top current is coming out at distance d and the bottom current is going in at distance d. d is now a radius.
so I tried
Also wrong. Tried to input it in various ways, ^(3/2), cancel out the pi's. Still wrong, "my answer is off by a multiplicative factor."
Help would be awesome!
Last edited: