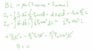Magnetic field of a rotating cylinder with permanent polarization

[astrocytosis]

Homework Statement

A long, solid dielectric cylinder of radius a is permanently polarized so that the polarization is
everywhere radially outward, with a magnitude proportional to the distance from the axis of the cylinder, $P = P_{0}r/2$
(a) Find the charge density in the cylinder.
(b) If the cylinder is rotated with a constant angular velocity $\omega$ about its axis without change in P, what is the magnetic field on the axis of the cylinder at point not too
near its ends?

Relevant Equations

Biot-Savart:

$B = \int \frac{J \times \hat{r}}{r^2} dV$
And $B = \int \frac{K \times \hat{r}}{r^2} da$

$J = \rho v$
$K = \sigma v$

$v = \omega s$ (s is the radius in plane of rotation)

I am struggling to get my work to match the posted solutions to this problem. I understand part (a) but can’t get the integral to work out for (b). I know I have to use Biot-Savart and add up the components from the the surface and volume currents. The cylinder is very long, so I need to make a change of variables to convert the integral over z into a integral over an angle from -pi/2 to pi/2. I should end up with a term that looks like cos(angle)d(angle) in place of dz. But instead I get

$\tan{\phi} = z/s$
$\sin{\phi} = z/r$

The second one is not insightful because it has r (distance from the point) in it, so using the first one

$dz = \sec{\phi}^2 s d\phi$

Then the volume integrand becomes (with j = -Po * omega * s)

$-P_{0} \omega \frac{s^2}{r^2} \sec{\phi}^2 ds d\phi d\theta$

But the problem is s/r is just the cosine, which cancels with the secant. What has gone wrong? Also, why can this problem not be solved using Ampere’s law? Are there any other ways of solving this problem?

I am also confused as to what is meant in part (b) by “along the axis of the cylinder.” This would seem to indicate the point is inside the cylinder, but if so how can the surface current be contributing?

I only have access to mobile today so formatting may be messed up. I attached a screenshot of the problem and my work with drawings that clarify the geometry (or my interpretation of it, anyway). I also attached the posted solution for clarity.

 

[astrocytosis]

Would this be a valid solution using Ampere’s law? Seems much simpler to do it this way...

also, I miscalculated the direction of the surface current before; I now see how it can contribute to the B field inside the cylinder

 

[TSny]

But the problem is s/r is just the cosine, which cancels with the secant. What has gone wrong?

In your handwritten notes, did you assume that $\vec j \times \vec r$ has a direction parallel to $\hat z$? That's only true for elements of current where $\phi = 0$.

I am also confused as to what is meant in part (b) by “along the axis of the cylinder.” This would seem to indicate the point is inside the cylinder, but if so how can the surface current be contributing?

The surface current acts like a solenoid. So, it will produce nonzero B on the axis.

 

[TSny]

Would this be a valid solution using Ampere’s law? Seems much simpler to do it this way...

Looks good to me. But, a complete solution should include some justification for your starting equation:

What Amperian path did you choose? Did you need to make any assumptions about the B field outside the cylinder?

 

[astrocytosis]

Thank you, I think I understand now; my mistake was I mixed up the r in Biot-Savart with the s in cylindrical coordinates

for a complete solution using Ampere’s law it must be assumed that B is zero outside (no fringing fields)