stunner5000pt
- 1,447
- 5
Griffith's problem 6.14
For a bar magnet make careful sketches of M(Magnetization) , B (Magnetic Field),and H (Griffith's just calls this H...), assume L = 2a.
Ok since ther is no free current here
and \oint \vec{H} \bullet d \vec{l} = I_{f(enclosed)}
H =0 yes??
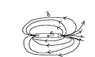
Check out my attached (bad) diagram. I drew the magnetic field. THe magnetization exists ONLY inside the magnet so it points in the direction from S to N. Since H = 0 it would not make an appearance... right?
For a bar magnet make careful sketches of M(Magnetization) , B (Magnetic Field),and H (Griffith's just calls this H...), assume L = 2a.
Ok since ther is no free current here
and \oint \vec{H} \bullet d \vec{l} = I_{f(enclosed)}
H =0 yes??
The Attempt at a Solution
Check out my attached (bad) diagram. I drew the magnetic field. THe magnetization exists ONLY inside the magnet so it points in the direction from S to N. Since H = 0 it would not make an appearance... right?