Magnetic Flux through a bent loop.

[Jnumen]

Homework Statement

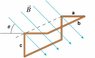
A 10cm x 10cm square is bent at a 90deg angle as shown in the figure.

A uniform 0.050T magnetic field points downdard at 45deg.

What is the magnetic flux through the loop.

Homework Equations

Flux= [(Aeff)*(B)].
Flux= [(Aeff)*(B)]*cos(theta).

The Attempt at a Solution

First I solved for the side due to the bend by using d= SQRT of [(a)^2*(c)^2].

Then, I calculated the Area using A= [(d)*(b)].

Then, I tried calculating with or without the 45deg angle using the following (which is not giving the correct answer):

Flux= [(Aeff)*(B)].
Flux= [(Aeff)*(B)]*cos(theta).

 

[Jnumen]

Does anyone know how I am supposed to treat the bend?

I have done problems when the area was flat, but I am not sure what I need to do differently when the area is bent. Isn't it going to decrease the area?

 

[Doc Al]

Does anyone know how I am supposed to treat the bend?

I have done problems when the area was flat, but I am not sure what I need to do differently when the area is bent. Isn't it going to decrease the area?

Two ways to go about it:

1) Treat it as two flat surfaces of area b*c and b*a. Find the flux through each of those surfaces and add them up.

2) Find the surface outlined by the by the two b sides. The angled piece doesn't matter, since the field is parallel to the bend. Sure the area changes, but so does the angle that the field makes with that surface.