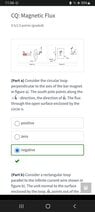
- #1
Flux from magnet (Why is the Flux not zero through the loop?)
In summary: The magnetic flux is negative when the angle between the field lines and the surface normal is greater than 90 degrees.
- #2
Frabjous
Gold Member
- 1,859
- 2,295
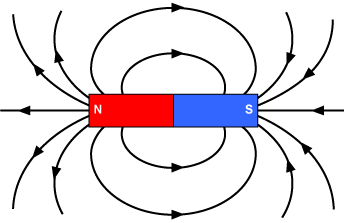
Here‘s a picture of the field lines. Why do you think the answer is zero?
- #3
member 731016
Thanks for your reply @Frabjous! because the number of field lines going into the loop is equal to the number going out.Frabjous said:
- #4
nasu
Homework Helper
- 4,442
- 894
This is an open surface. There is no in and out. These apply only to closed surfaces. You should review the definition of flux through a surface. According to your idea, the flux would be always zero.
- #5
Frabjous
Gold Member
- 1,859
- 2,295
The flux is a measure of the net amount going through a surface. What equation are you using for flux?
- #6
- #7
Frabjous
Gold Member
- 1,859
- 2,295
What is the sign of cosθ for the surface of interest? Hint: the normal to the surface is pointing to the right. The B field is pointing to the left.
Last edited:
- #8
member 731016
Thanks for your reply @Frabjous ! I think the direction of the B-field relative to the surface normal varies along the surface.Frabjous said:
Many thanks!
- #9
Frabjous
Gold Member
- 1,859
- 2,295
Yes it varies, but it is all the same sign. What is the sign?
- #10
member 731016
Thanks for your reply @Frabjous ! I think the sign is negative because ##\theta > 90 ## so ##\cos\theta < 0 ##Frabjous said:
Thanks again, I see why the magnetic flux is negative now.
FAQ: Flux from magnet (Why is the Flux not zero through the loop?)
Why is the magnetic flux through the loop not zero?
The magnetic flux through a loop is not zero when there is a magnetic field passing through the area enclosed by the loop. This is because magnetic flux is defined as the product of the magnetic field strength, the area it penetrates, and the cosine of the angle between the field and the normal to the surface. If any of these factors are non-zero, the flux will also be non-zero.
How does the orientation of the loop affect the magnetic flux?
The orientation of the loop affects the magnetic flux because the flux depends on the angle between the magnetic field and the normal (perpendicular) to the surface of the loop. If the loop is oriented such that the magnetic field is perpendicular to the plane of the loop, the flux is maximized. If the loop is parallel to the field, the flux is zero. For other angles, the flux is proportional to the cosine of the angle between the field and the normal to the loop.
What role does the area of the loop play in determining the magnetic flux?
The area of the loop is directly proportional to the magnetic flux. A larger loop area allows more magnetic field lines to pass through, resulting in a higher flux. Conversely, a smaller area results in fewer field lines passing through, leading to a lower flux. The relationship is given by the equation: flux = B * A * cos(θ), where B is the magnetic field strength, A is the area, and θ is the angle between the field and the normal to the loop.
Can a changing magnetic field affect the flux through the loop?
Yes, a changing magnetic field can affect the flux through the loop. According to Faraday's Law of Electromagnetic Induction, a time-varying magnetic field induces an electromotive force (EMF) in the loop, which is proportional to the rate of change of the magnetic flux. This means that even if the loop is stationary, a changing magnetic field will result in a changing flux through the loop.
Why is the flux not zero even if the magnetic field is uniform?
Even if the magnetic field is uniform, the flux through the loop can still be non-zero because the flux depends on the presence of the magnetic field, the area of the loop, and the orientation of the loop relative to the field. As long as the magnetic field lines pass through the loop and the area is not zero, the flux will be non-zero. The uniformity of the field ensures that the field strength is constant, but it does not negate the existence of the flux.