Magnitude of charge on parallel plates

[Melssssss]

Homework Statement

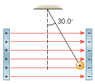
A small plastic ball of mass 7.51 × 10-3 kg and charge +0.123http://edugen.wileyplus.com/edugen/courses/crs6407/art/qb/qu/c18/lower_mu.gifC is suspended from an insulating thread and hangs between the plates of a capacitor (see the drawing). The ball is in equilibrium, with the thread making an angle of 30.0o with respect to the vertical. The area of each plate is 0.02109 m2. What is the magnitude of the charge on each plate?

Homework Equations

electric field= q/EoA
electric force= qE

The Attempt at a Solution

I have found the electric field and the force from above equations, I just get lost on how to go from here.

 

[TSny]

Welcome to PF!

I have found the electric field and the force from above equations, I just get lost on how to go from here.

You've done the hard work! Hopefully you've studies how the charge on the plates of a parallel plate capacitor is related to the electric field between the plates.

 

[Melssssss]

Welcome to PF!

You've done the hard work! Hopefully you've studies how the charge on the plates of a parallel plate capacitor is related to the electric field between the plates.

are you talking about the capacitance? That's the next chapter and isn't related to this problem

 

[TSny]

Look at the first equation you wrote under the section "Relevant equations" in your first post.

 

[Melssssss]

yes but how is the mass and the angle come into play?

 

[TSny]

yes but how is the mass and the angle come into play?

Those come into play in finding the electric field, which you said that you already did.

 

[Melssssss]

by using the equation I gave, which only uses the area and charge,

 

[cnh1995]

I have found the electric field and the force from above equations, I just get lost on how to go from here.

You took q as the charge on the mass while the formula Q/εA uses the charge on the plates of the capacitor, which is unknown.
I believe an FBD would be helpful here.

 

[Melssssss]

This is the picture provided.

 

[cnh1995]

This is the picture provided.

What are the forces acting on it? Can you write the equations of forces along horizontal and vertical directions? For that you'll need mass and the angle..

 

[Melssssss]

the forces would be tension, weight of the ball and electric force.
so since the ball is at equilibrium the net forces are equal.
so if tension is pulling up and gravity down, tension is also pulling left and the electric force right.
so if I find the tension would this be equal to the electric force?

 

[cnh1995]

so if I find the tension would this be equal to the electric force?

No. Tension is pulling the ball at an angle 30 degrees with the vertical. Electrical force is horizontal and weight of the ball is downward. The net force is 0. How will you write the equations for vertical and horizontal components of the forces?

 

[Melssssss]

Tsin 30= mg

 

[cnh1995]

Tsin 30= mg

30 degrees angle is with the vertical.. It should be Tsin60=mg...
What about horizontal forces?

 

[Melssssss]

electric force is pulling to the right and tension is also pulling to the left slightly but I am unsure how I would make that an equation

 

[cnh1995]

Tsin60=mg...

What is the horizontal component of tension? Equate it to electrical force.

 

[Melssssss]

Tsin(theta)= electric force?

 

[Melssssss]

Tsin(theta)= electric force?

sorry t cos(theta)

 

[cnh1995]

sorry t cos(theta)

Right..theta=60 degrees.. You just resolved tension into two components which balance the horizontal electrical force and downward weight. Now, what will you do to get rid of T from both the equations?

 

[Melssssss]

well you can solve for T from the first equation since you know the mass and gravity. then plug it into the 2nd equation.

 

[cnh1995]

Right. (Or you can take the ratio of both) You then have only one unknown left, i.e. electric field. From that electric field, you can calculate the charge on the capacitor plates.
Good luck!