dl447342
- 28
- 5
- Homework Statement
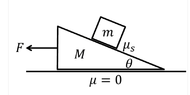
- A block of mass m sits on a wedge of mass M, which is free to move along a horizontal surface with negligible friction. The coefficient of static friction between the block and the wedge is ##\mu_s##. A horizontal force of a magnitude ##F## pulls on the wedge, as shown in the attached diagram. When ##\tan \theta > \mu_s##, which of the following are true:
A) The force F must be directed to the right with a minimum magnitude.
B) The force F must be directed to the right with a maximum magnitude.
C) The block will slip even if ##F=0##.
- Relevant Equations
- Newton's second laws are crucial here. From drawing a free-body diagram, one can deduce that the static friction force ##f_s## satisfies ##f_s = m(g\sin \theta +\frac{F}{M+m} \cos\theta) \leq \mu_s m(g\cos\theta - \frac{F}{m+M} \sin\theta)## and that the required maximum force is ##\frac{\mu_s -\tan\theta}{1+\mu_s \tan\theta}(M+m)g ## (I'm stating this because the key part of this question is to determine which of the three statements are correct; I've already figured out the free-body diagrams and Newton's equations).
Clearly if ##F = 0## and ##\tan\theta > \mu_s##, then using the above equations for ##f_s## and ##n##, we get ##f_s > \mu_s n## so the block will slip. However, it seems that as long as the force ##F## is directed to the right with a certain minimum magnitude, namely ##\frac{\tan\theta - \mu_s}{1+\mu_s \tan\theta}(M+m)g##, the block won't slip.
Is this reasoning right?
Is this reasoning right?