SUMMARY
The forum discussion centers on the calculation of line charge density in power lines, specifically addressing the confusion surrounding the use of voltage equations. The user initially struggled with the correct formulation, mistakenly using the equation ##\Delta V = -E\,r## instead of the more accurate ##dV = -E\,dr##. The community provided guidance, leading to the user's successful resolution of the issue and appreciation for the support received.
PREREQUISITES
- Understanding of electric fields and voltage relationships
- Familiarity with calculus, particularly differentiation
- Basic knowledge of LaTeX for mathematical expressions
- Concept of line charge density in electrostatics
NEXT STEPS
- Study the derivation of electric field equations in electrostatics
- Learn how to effectively use LaTeX for formatting mathematical equations
- Explore the concept of line charge density and its applications in power systems
- Investigate the relationship between electric fields and potential differences in various geometries
USEFUL FOR
Students and professionals in electrical engineering, physics enthusiasts, and anyone involved in the study of electrostatics and power line analysis.
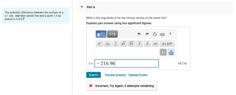
 ##\qquad## !
##\qquad## !