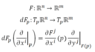Graduate Making sense of the Differential of F at p, (where F: R^n -> R^m)

[bigbalpha]

TL;DR

I understand dFp as the jacobian (matrix of derivatives of F) but this specific relation shown below I am having a hard time understanding when I think of it in terms of matrix multiplication as an operator on a vector.

Here is a snip of the fundamental relation:

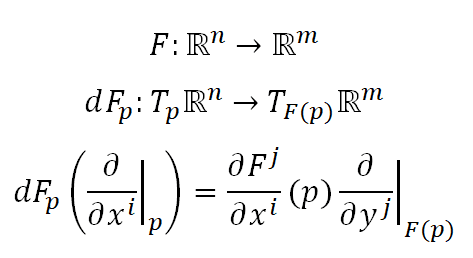
This is from the book "Intro to Smooth Manifolds" and in this section it is simplified down to F as a map between just the real spaces R^n -> R^m (as shown above).
I understand the meaning of this relation, as the following: The rightside is the vector in the codomain of dFp, where the jacobian values are the components of the vector along the basis d/dy^j, mapped by dFp, from the i'th basis vector in the domain.

To my understanding, the rightside has an implied sum over the index j (1 - m), and i is a free index on both sides.

Fundamentally, the symmetry of this relation is what is confusing me. dFp is an operator, on vectors in the domain. This makes it a matrix (jacobian matrix), then how come there isn't an implied sum, just as on the rightside? And then what is the difference between the symbol dFp on the left, and the double-indexed derivative on the right (dF^j/dx^i), both are the jacobian matrix acting on vectors, right?

 

[fresh_42]

Fundamentally, the symmetry of this relation is what is confusing me. dFp is an operator, on vectors in the domain. This makes it a matrix (jacobian matrix), then how come there isn't an implied sum, just as on the right side?

Because it is the formula for the $i-$th component, not the entire vector: $w_i=A^j_iv_j$.

And then what is the difference between the symbol dFp on the left, and the double-indexed derivative on the right (dF^j/dx^i), both are the jacobian matrix acting on vectors, right?

Yes, but the Jacobian matrix is the coordinate form, whereas $dF_p$ only names the operator, regardless which coordinates are chosen.

If you like you can read our essay about it:
https://www.physicsforums.com/insights/the-pantheon-of-derivatives-i/