Mass connected with three springs-Oscillations

[Tanya Sharma]

Homework Statement

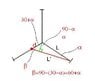
A particle of mass m is attached to three springs A , B , C of equal force constants k as shown in the figure.The angle between each pair of springs is 120° initially . If the particle is pushed slightly against the spring C and released, find the time period of oscillation.

Homework Equations

The Attempt at a Solution

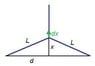
Let the particle be displaced from O to P .i.e OP=x . Spring C is compressed by distance x .Spring A is stretched by a distance PA - OA . Spring B is stretched by a distance PB - OB.
Perpendicular OX and OY are dropped on PA and PB respectively . For small displacement BY ≈ BO and AO ≈ AX .So, PX is approximately extension in spring A .PX=POsinα or PX=POcosβ .

Now , how do I determine the angle α or β so that I may proceed with the problem ?

 

[ehild]

The distance PO is given, say d. You can find PA with the Law of Cosines. (The angle POA is 120°. )

ehild

 

[Tanya Sharma]

Let the length of spring be L
OA≈XA =L

If we consider ΔOPA then L^2 = d^2 + (PX + L)^2 - 2d(PX+L)Cosβ

PX is the stretching in spring which is ultimately what we are trying to find and is an unknown and so is L .How will we get a definite value of β ? β should turn out to be 60° .

 

[Saitama]

Let the length of spring be L
OA≈XA =L

If we consider ΔOPA then L^2 = d^2 + (PX + L)^2 - 2d(PX+L)Cosβ

PX is the stretching in spring which is ultimately what we are trying to find and is an unknown and so is L .How will we get a definite value of β ? β should turn out to be 60° .

There is no need of introducing β. Use Law of Cosines as ehild pointed out.

 

[ehild]

You need to find the resultant force acting on the point mass which is displaced towards C, say, with distance d. The spring C exerts force of magnitude kd, the other strings exert forces of magnitude k(L'-L) where L' is the stretched length of the springs connected to A and B. L' can we obtained with the Cosine Law.
These forces act along the springs, and you need the component parallel with spring C which is k(L'-L)cos(β). β is very close to 60°.

ehild

 

[Tanya Sharma]

ehild...thank you very much

 

[ehild]

Have you solved the problem? What is the result?

ehild

 

[Tanya Sharma]

Force due to spring C=kd
Component of Force due to spring A =k(xsin60°)(cos60°)=kd/4
Component of Force due to spring A =k(xsin60°)(cos60°)=kd/4

Total restoring force =(3/2)kd

Effective force constant = (3/2)k

Time period = 2∏(√(2m/3k)) which is the correct answer .

The problem for me was to get the stretching in the springs . Though I still haven't been able to apply Law of Cosines .I found the stretching from isosceles triangle OXA .Angles opposite to equal sides must be equal , hence ∠AOX=90° .Now∠AOP=120° .So ∠POX =30° .

If I apple Law of cosines in ΔAOP

L'² = L² + d² -2(d)(L)cos120°

L'² = L² + d² +(d)(L)

Now I am stuck here ?

 

[ehild]

The problem for me was to get the stretching in the springs . Though I still haven't been able to apply Law of Cosines .I found the stretching from isosceles triangle OXA .Angles opposite to equal sides must be equal , hence ∠AOX=90° .Now∠AOP=120° .So ∠POX =30° .

What you have shown in post #1 is not an isosceles triangle if the angle is 90°, or if it is isosceles triangle the angle is not 90°. But you are right , the angles at the base of a very elongated isosceles triangle can be approximated by 90°. It is a usual approximation, and the solution is correct.
What I suggested, it would have been a more rigorous derivation, applying calculation with small quantities. That means keeping only the linear terms of a small quantity, and using some approximate formulas, useful to remember:

1/(1+δ) a≈1-δ, √(1+δ)≈1+δ/2, sin(δ)≈δ, cos(δ)≈1.

(They follow from the Taylor expansion, stopping at the linear term.)

If I apple Law of cosines in ΔAOP

L'² = L² + d² -2(d)(L)cos120°

L'² = L² + d² +(d)(L)

Now I am stuck here ?

L'= L²(1 + d²/L² +d/L)

δ=d/L <<1, its second power can be ignored, and applying √(1+δ)=1+δ/2, L'=L(1+d/(2L))

The stretching of the spring is L'-L=d/2. It should be multiplied by cos(β. You can show that β=pi/3-α. sin(α) is some multiple of d/L, a small quantity, cos(α)≈1, so cos(β)≈1/2+√3/2sin(α).
It is multiplied by d/L,

d/(2L)(1/2+√3/2sin(α))=d/(4L) +a second-order small quantity, ≈d/4L.

ehild

 

[Tanya Sharma]

Thanks for the wonderful explanation It had never crossed my mind there was so much going behind the scenes .

You have been kind enough to explain the maths .

I am trying to learn some maths here , so was unable to comprehend certain things...

. You can show that β=pi/3-α. sin(α) is some multiple of d/L, a small quantity.

How?

, so cos(β)≈1/2+√3/2sin(α).

How did we get the second term ? Shouldnt it be negative ?

It is multiplied by d/L,

d/(2L)(1/2+√3/2sin(α))=d/(4L) +a second-order small quantity, ≈d/4L.

ehild

Why are we multiplying with d/L ?

 

[ehild]

β=π/3-α . See picture. You can understand that alpha decreases with d. If d is very small with respect to L, so is alpha (with respect to pi)
You need the component of k(L'-L), which is cos(β)k(L'-L).

cos(pi/3-α)=cos(π/3)cosα-sin(π/3)sin(-α)=cos(π/3)cosα+sin(π/3)sinα.

k(L'-L)=kd/2. I made an error here in the previous post.

So the component of force from string A is k(d/2)cosβ=k(d/2)(1/2+√3/2 sinα) ≈ kd/4 as sinα is a very small quantity.

ehild

 

[Tanya Sharma]

Thanks ehild...You have explained the maths behind the problem very nicely

 

[TSny]

Another approach (not necessarily any better).

See attached figure which shows the three springs in the initial configuration rotated so that spring C is vertical.

Suppose x is increased by dx. Taking differentials of L² = x² + d² gives 2LdL = 2xdx, so dL = (x/L)dx. Using x/L = 1/2 in the initial configuration yields dL = dx/2.

So, if spring C is compressed by dx, the other two springs stretch by dx/2.

 

[ehild]

Nice explanation, TSny!

ehild