- #1
eedftt
- 9
- 0
- Homework Statement
- Mastering Physics
- Relevant Equations
- Magnetic Field
Magnetic fields are sometimes measured by balancing magnetic forces against known mechanical forces. Your task is to measure the strength of a horizontal magnetic field using a 12-cm-long rigid metal rod that hangs from two nonmagnetic springs, one at each end, with spring constants 1.3 N/m
. You first position the rod to be level and perpendicular to the field, whose direction you determined with a compass. You then connect the ends of the rod to wires that run parallel to the field and thus experience no forces. Finally, you measure the downward deflection of the rod, stretching the springs, as you pass current through it. Your data are as follows:
Graphing either Δy versus I or I versus Δy gives a straight line. In the graph shown, we chose to plot Δy on the vertical axis and I on the horizontal axis. From the equation for the line of best fit given, determine the magnetic field strength B
.
Express your answer to two significant figures and include the appropriate units.
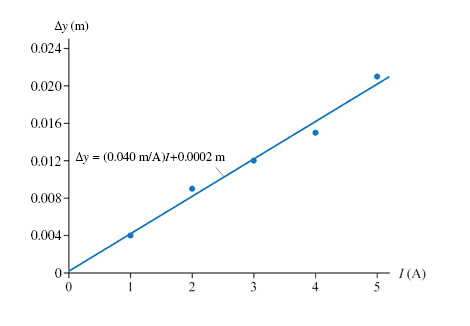
According to BIL = 2k*∆y
The slope is BL/(2k)
B = 2 * slope * k / (L) = 0.87
However, the system told me it was wrong.
. You first position the rod to be level and perpendicular to the field, whose direction you determined with a compass. You then connect the ends of the rod to wires that run parallel to the field and thus experience no forces. Finally, you measure the downward deflection of the rod, stretching the springs, as you pass current through it. Your data are as follows:
| Current, I(A) |
| Deflection Δy(mm) |
1.0 | 4 |
2.0 | 9 |
3.0 | 12 |
4.0 | 15 |
5.0 | 21 |
.
Express your answer to two significant figures and include the appropriate units.
According to BIL = 2k*∆y
The slope is BL/(2k)
B = 2 * slope * k / (L) = 0.87
However, the system told me it was wrong.