Math Behind Why a Box Tips Over When x > b/2

[Drain Brain]

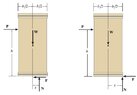
I just want to know the correct mathematical workings of why the box will tip over when distance x of the normal force from the center line is b/2.

what I know is when $\sum M$ about the point of application of the normal force is zero, the box will not tip over.

so, mathematically $W\frac{b}{2}=Ph$

it means that when $x\le\frac{b}{2}$ the box will not tip over. is that correct?

What if the point of application of the normal force is at the center line (i.e x=0)? and What if $x>\frac{b}{2}$?
can you show me mathematically what will happen? Thanks!

 

[I like Serena]

it means that when $x\le\frac{b}{2}$ the box will not tip over. is that correct?

It's the other way around. The smaller $x$ is, the easier will the box tip over.
That's because the weight is responsible for keeping it in balance, tilting the box back to the left.

What if the point of application of the normal force is at the center line (i.e x=0)? and What if $x>\frac{b}{2}$?
can you show me mathematically what will happen? Thanks!

The sum of the moments with respect to the point where the normal force is applied is:
$$M_{\text{total with respect to N}} = \sum M_{\text{with respect to N}} = -W\cdot x + P \cdot h$$
That is assuming the we consider counter clockwise a positive rotation.

If $M_{\text{total with respect to N}} \ge 0$ the box will not tip over since it will want to rotate to the left.