Mathematical conundrum when adding complex exponentials

[Runei]

Hi there,

Once again I find myself twiddling around with some quantum mechanics, and I bumped into something I find strange. I can't see what the error of my thinking is, so I hope someone could be able to point it out.

I'm looking at solutions to the infinite square well, and arrive at the simple differential equation

$$\frac{d^2\Psi}{dx^2} = -k^2 \Psi$$

The solution to this can be written in terms of complex exponentials or sines and cosines. I bumped into the weird stuff when I use complex exponentials.

So the general solution in that case would be

$\Psi(x) = Ae^{ikx}+Be^{-ikx}$

Now, what I then started thinking was: "Hmmm... This could be viewed mathematically as a sum of two vectors, and solution is simply another vector."

So I drew this picture to illustrate the idea:

​

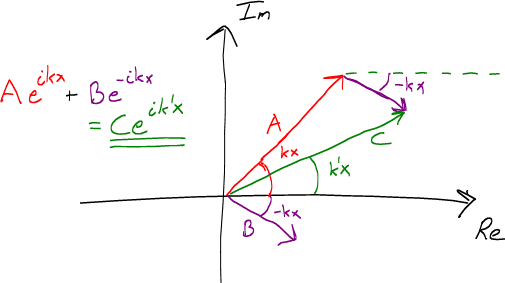
So from that perspective it seems that the solution could also be written as

$\Psi(x) = Ce^{ik'x}$

However, using the simple constraints of the infinite square well quickly leads to problems - namely:

$|\Psi(0)|^2 = 0$

$C = 0$

So... Now really what I had hoped for. Where am I going taking a wrong turn? Has it to do with the x? That x should be x' also?

Thanks in advance :)

 

[Orodruin]

The problem is that your $k'$ is going to be a function of $x$. As such, you can not assume it to be constant and apply derivatives to the wave function with that assumption.

 

[Strilanc]

Consider that $e^{ix} + e^{-ix}$ is equal to $2 cos(x)$ and so has no net imaginary component for all x. But a single $e^{kix}$ always has some net imaginary component (for finite $k$ and $x$).

 

[Runei]

Thanks guys!

I gave it some more thought and think I nailed it down now.

I have another question now thought, but I'm going to make another thread for it.