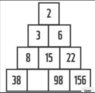
Undergrad Maths puzzle -- What is the missing digit?

[engnrshyckh]

TL;DR

Its a puzzle i can not able to solve it

In the fig attached we have to find what will be the digit in the missing box i can't figure it out

 

[.Scott]

@engnrshyckh:

I will give you these clues:
1) The pyramid shape is irrelevant. The sequence 2, 3, 6, 8, 15, 22, 38, x, 98, 156 is sufficient.
2) If the terms are labelled $A_0=2$, $A_1=3$, $A_2=6$, etc; then the even A's are computed with a slightly different formula than the odd A's.
3) $A_{-1}$ is not zero.

 

[.Scott]

@engnrshyckh: Let me know if you've cracked it or need more assistance.

 

[engnrshyckh]

@engnrshyckh:

I will give you these clues:
1) The pyramid shape is irrelevant. The sequence 2, 3, 6, 8, 15, 22, 38, x, 98, 156 is sufficient.
2) If the terms are labelled $A_0=2$, $A_1=3$, $A_2=6$, etc; then the even A's are computed with a slightly different formula than the odd A's.
3) $A_{-1}$ is not zero.

Still i am not sure how to solve it. Is it some kind of arithmetic sequence or geometric sequence?

 

[mfb]

You can calculate the differences between two subsequent numbers and check if these are somehow linked to other elements in the sequence.

 

[willem2]

2) If the terms are labelled A₀=2, A₁=3, A₂=6, etc; then the even A's are computed with a slightly different formula than the odd A's.

While i did use this initially to find the solution, you can also give a single equation valid for both even and odd A's. (and no (-1)^n or anything like that in it)

 

[.Scott]

While i did use this initially to find the solution, you can also give a single equation valid for both even and odd A's. (and no (-1)^n or anything like that in it)

Using $(-1)^n$ obviously works. I also think there is a way to use absolute value. But for the purpose of providing a clue, those aren't very useful.To @engnrshyckh:
Here are a couple of additional clues:
4) One way of identifying a sequence that grows exponentially is to list the ratios between consecutive elements. If you do this with the Fibonacci sequence, you will see that the ratio approaches 1.618034, the Golden Ratio, $\frac{1+\sqrt{5}}{2}$. If your sequence also closes on a ratio, then it is also exponential. However, note that, although the Fibonacci series is exponential, no exponential function is used to compute its elements.
5) After the 156, the next 10 numbers in the sequence are: 255, 410, 666, 1075, 1742, 2816, 4559, 7374, 11934, and 19307.

If you solve it, let us know. If you don't, show the results you got by applying the exponential test I described above.

 

[willem2]

Using $(-1)^n$ obviously works. I also think there is a way to use absolute value. But for the purpose of providing a clue, those aren't very useful.

I said i was not using that.
You can however get an exact formula for the n-th element of the series, and it does involve (-1)^n.
If you type [insert recurrence relation here], a(0)=2, a(1)=3, a(2) = 6 in wolfram alpha, you'll get the exact solution.

However, note that, although the Fibonacci series is exponential, no exponential function is used to compute its elements.

There is an exact non-recursive formula for the elements of the Fibonacci series, which does use the exponential function.

 

[.Scott]

If you type [insert recurrence relation here], a(0)=2, a(1)=3, a(2) = 6 in wolfram alpha, you'll get the exact solution.

I see. You go back one more term to get the even/odd information.
The absolute value method that I had in mind actually generated the sequence -2, 3, -6, 8, -15, 22, ...
Then you needed to take the absolute value of those terms to get the target sequence.

I like your method better.

 

[phinds]

You can calculate the differences between two subsequent numbers and check if these are somehow linked to other elements in the sequence.

Clever. I missed that

 

[engnrshyckh]

While i did use this initially to find the solution, you can also give a single equation valid for both even and odd A's. (and no (-1)^n or anything like that in it)

These are successive ratio 1.5,2,1.333,1. 875 but these are not the same as in geometric propagation.

 

[DrClaude]

These are successive ratio 1.5,2,1.333,1. 875 but these are not the same as in geometric propagation.

Why are you calculating ratios?

You can calculate the differences between two subsequent numbers and check if these are somehow linked to other elements in the sequence.

 

[engnrshyckh]

Why are you calculating ratios?

Difference is not the same also 1,3,2,7,7... To use arithmetic propagation farmula

 

[PeroK]

Difference is not the same also 1,3,2,7,7... To use arithmetic propagation farmula

Here's a clue: it's not a Fibonacci sequence!

 

[mfb]

... but it's quite close. Might be interesting to calculate the difference in each case...?

 

[engnrshyckh]

Here's a clue: it's not a Fibonacci sequence!

118 is the correct ans thanks for the help

 

[engnrshyckh]

118 is the correct ans thanks for the help

If i am not wrong

 

[PeroK]

118 is the correct ans thanks for the help

It can't be $118$. That's too big.

 

[.Scott]

These are successive ratio 1.5,2,1.333,1. 875 but these are not the same as in geometric propagation.

OK. But I gave you several more numbers in the sequence. Calculate all of the ratios for pairs up to 19307/11934. What you will discover is that it IS an exponential sequence - very similar to Fibonacci.

 

[engnrshyckh]

It can't be $118$. That's too big.

Then what i am missing?

 

[.Scott]

Why are you calculating ratios?

He's calculating ratios because it is a possible method for detecting an exponential sequence (suggested by me). The only proble is that he didn't calculate enough of them. The will close on the Golden Ratio - a significant clue to how the sequence can be generated.

 

[PeroK]

Then what i am missing?

How does 118 work out? I don't see the pattern.

 

[engnrshyckh]

OK. But I gave you several more numbers in the sequence. Calculate all of the ratios for pairs up to 19307/11934. What you will discover is that it IS an exponential sequence - very similar to Fibonacci.

Yes its an exponential sequence but i am unable to find its equation which gives the correct answer

 

[PeroK]

He's calculating ratios because it is a possible method for detecting an exponential sequence (suggested by me). The only proble is that he didn't calculate enough of them. The will close on the Golden Ratio - a significant clue to how the sequence can be generated.

I have something a lot simpler! Are there two answers?

 

[.Scott]

It is not 118.
Clue #6: The portion of the sequence that we are working with is monotonically increasing. So it is between 38 and 98.

 

[engnrshyckh]

How does 118 work out? I don't see the pattern.

I used method of difference see the picture

 

[.Scott]

Yes its an exponential sequence but i am unable to find its equation which gives the correct answer

It's not just an exponential equation. The ratio is the about the same as for the Fibonacci Series. So you should ask - how does the formula for generating the next Fibonacci number ($v_i = v_{i-1} + v_{i-2}$) result in the Golden Ratio?

 

[engnrshyckh]

It's not just an exponential equation. The ratio is the about the same as for the Fibonacci Series. So you should ask - how does the formula for generating the next Fibonacci number ($v_i = v_{i-1} + v_{i-2}$) result in the Golden Ratio?

Enlighten me i shall be greatfull

 

[PeroK]

One last clue:

$2 + 3 \approx 6$
$3 + 6 \approx 8$
$6 + 8 \approx 15$

 

[.Scott]

We're not suppose to just give you the solution. So here's another (hopefully final) clue:

We know (2, 3, 6, 8, 15, ...) isn't Fibonacci because:
6 <> 2+3 (just misses)
8 <> 3+6 (just misses)
15 <> 6+8 (just misses)
22 <>