Matrix Chain Multiplication: Optimal way of multiplying

[zak100]

Hi,

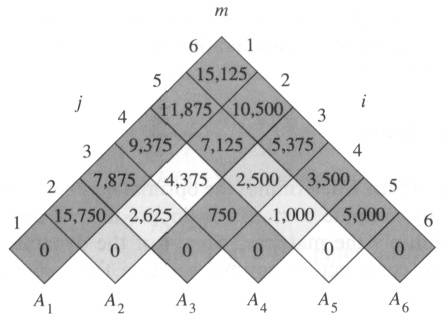
I am studying Matrix chain Multiplication to find out the optimal way of multiplying a series of matrices so that we can reduce the number of multiplications. I have got this example from the book which multiplies the matrices having dimensions given below:

A1 30 * 35

A2 32 * 15

A3 15 * 5

A4 5 * 10

A5 10 * 20

A6 20 * 25

From these matrices, it creates the 2 tables:

The algorithm is given below:

MTM(A, s, I, j)

If j> i

Then Xß MCM(A, s, I, s[I,j])

Y ß MCM(A, s, s[I,j] + 1, j)

return MCM (X, Y)

else return Ai

They are invoking the algorithm by:

MCM(A, s, 1, 6)

Can some body guide me what is the value of A & s?
After that i want to find out the best way of ordering these matrices for multiplication. Some body please guide me.
Zulfi.

 

[SlowThinker]

I guess the book should explain this?

If I'm reading the algorithm correctly, it multiplies t=A1*A2, t=t*A3, s=A5*A6, s=A4*s, t=t*s, return t. This seems to comply with the intuitive idea of picking the longest "edge" available:
first 35 between A1 and A2,
then 20 between A5 and A6,
then 15 between (A1*A2) and A3,
then 10 between A4 and (A5*A6),
and last 5 between (A1*A2*A3) and (A4*A5*A6).
The s-table is a way to drive the calculation, even though it seems a bit complicated. The m-table is probably used to fill in the s-table, and that should be explained in the book you're reading.

Just a side note, if you want to get anywhere in programming, you *absolutely can not* afford typing errors. I is not i, A is not m, 32 is not 35, and MCM is not MTM.

 

[zak100]

Hi,
I am correcting my algorithm. I can't find edit option:
1. MCM(A, s, i, j)
2. if j> i
3. then X= MCM(A, s, i, s[i,j])
4. Y = MCM(A, s, s[i,j] + 1, j)
5. return MCM (X, Y)
6. else return Ai

Kindly tell me how to evaluate this algorithm.

Zulfi.

 

[Mark44]

Hi,
I am correcting my algorithm. I can't find edit option:
Mod note: added code tags to preserve original indentation

1. MCM(A, s, i, j)
2. if j> i
3.        then X= MCM(A, s, i, s[i,j])
4.                 Y = MCM(A, s, s[i,j] + 1, j)
5.                 return MCM (X, Y)
6. else return Ai

Kindly tell me how to evaluate this algorithm.

You don't "evaluate" an algorithm -- you (or the computer) perform the steps in the algorithm.
Step 1. What does MCM(A, s, i, j) mean? What action is performed by this step? What are A and s, and what are the values of i and j? Are A and s two-dimensional arrays?
Step 2. Are the values of i and j known? If not, how can anyone know whether j > i or i < j or i == j?
Step 5. What does MCM(X, Y) mean? What are X and Y? In steps 1, 3, and 4, MCM takes four arguments. In this step there are only two arguments.
Step 6. What is Ai?

 

[zak100]

Hi,
Thanks for taking interest in my problem.
MCM means Matrix Chain Multiplication & 4 arguments are passed to this algorithm
<
You don't "evaluate" an algorithm -- you (or the computer) perform the steps in the algorithm.
>
I have to evaluate the value return by algorithm by tracing the steps mentioned in it. Its a recursive algorithm. I am doing some tracing work but it I get confused because of the two recursive calls & X & Y will get what value returned by the recursive function.<
Are the values of i and j known? If not, how can anyone know whether j > i or i < j or i == j?

>
Yes I have to call: MCM(A,s,1,6), A & s are shown in the figure which are two tables accessed by i & j
Therefore i=1 & j=6
<
What does MCM(X, Y) mean? What are X and Y? > Sorry this is again a mistake,
1. MCM(A, s, i, j)
2. if j> i
3. then X= MCM(A, s, i, s[i,j])
4. Y = MCM(A, s, s[i,j] + 1, j)
5. return MatrixMultiply (X, Y)
6. else return Ai

This means X & Y are matrices & i have shown their rows & columns above. Again:
A1 30 * 35
A2 35 * 15
A3 15 * 5
A4 5 * 10
A5 10 * 20
A6 20 * 25Thus i want to a know a better method or technique for evaluating (i.e. to find out the value returned by) this recursive function.

Zulfi.

 

[zak100]

Hi,
I mentioned the invoking statement in my first post also:
<
They are invoking the algorithm by:

MCM(A, s, 1, 6)

Can some body guide me what is the value of A & s?
After that i want to find out the best way of ordering these matrices for multiplication. Some body please guide me.
Zulfi.
>

Zulfi.

 

[SlowThinker]

They are invoking the algorithm by:

MCM(A, s, 1, 6)

Can some body guide me what is the value of A & s?

$A$ is an array of the input matrices. For example, A[3] is a matrix of 15*5 elements.
$s$ is a 2-dimensional array, with values as given in the picture in your first post. The elements that are not shown, such as s[4,2], are not used by the algorithm, so the value of these elements is not important.

 

[zak100]

Hi,
My friend thanks for your reply.
<A is an array of the input matrices. For example, A[3] is a matrix of 15*5 elements.>
I don't think so because the book has shown the values of A1-A6 in terms of its dimensions. We have to use these dimensions to find out the optimal way of multiplying these matrices.
<
s is a 2-dimensional array, with values as given in the picture in your first post. The elements that are not shown, such as s[4,2], are not used by the algorithm, so the value of these elements is not important.>
No my friend 's' table is very important. That's why book has shown it. I have Solved this problem using recursion tree. Thanks all.

Zulfi.

 

[zak100]

Hi,
Sorry for wrongly correcting you. I agree with you.

<A is an array of the input matrices. For example, A[3] is a matrix of 15*5 elements.>
The above is correct. Dimensions are stored in another set of variables: p0 to p6 & this is mentioned in another algorithm which is used to create 'm' table.

Thanks for your time.

Zulfi.