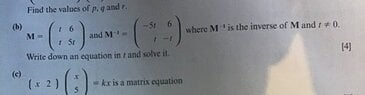The discussion focuses on solving a matrix equation related to the IGCSE curriculum, specifically the equation $[M]^{-1} \cdot [M] = [I]$. The matrices involved are $[M] = \begin{bmatrix} -5t & 6\\ t & -t \end{bmatrix}$ and its inverse. Participants are encouraged to multiply the matrix $[M]^{-1}$ by $[M]$ and equate the resulting matrix to the identity matrix $[I] = \begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix}$, leading to a system of equations in terms of the variable $t$. This method is essential for finding the value of $t$ that satisfies the equation.
PREREQUISITESStudents preparing for the IGCSE mathematics exam, particularly those focusing on linear algebra and matrix operations.
