Maximally symmetric sub-manifold (2-sphere)

[Apashanka]

Again in pg. 166 eq 7.2
https://www.google.com/url?sa=t&sou...FjACegQIBhAB&usg=AOvVaw1YY2mM7uccdbX4nTxFgQO5

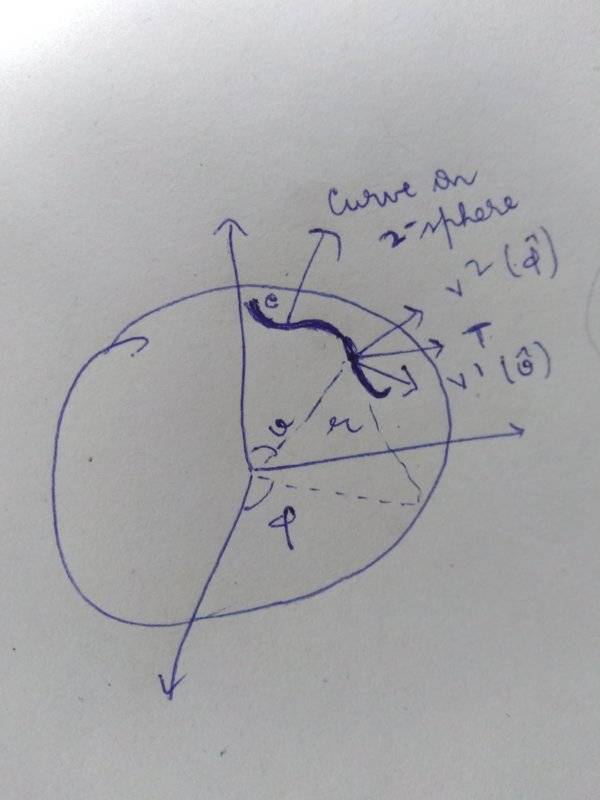
Here $u^1=\theta,u^2=\phi$ and v=r.
The tangent vector on the sub-manifold points on $V^1 \hat \theta$ & $V^2 \hat \phi$.
It is written here to get rid of cross terms the tangent vectors$\frac{∂}{∂V^I}$ (here $\frac{∂}{∂r}$) is made perpendicular to the submanifolds.
Can anyone please explain what is the last line trying to say and how it will be applicable here??

 

[Apashanka]

Another, if we consider our 3-D space foliated by 2-sphere then the metric becomes $ds^2=f_1(r)dr^2+f_2(r)d\Omega^2$
where $d\Omega^2=d\theta^2+sin^2\theta d\phi^2$
But our known metric is $dr^2+r^2d\Omega^2$ and comparing this two we get $f_1(r)=1$ and $f_2(r)=r^2$,my question how are these $f_1(r)$ and $f_2(r)$ are determined??

 

[PeterDonis]

The tangent vector on the sub-manifold

Tangent vector to what? You have drawn a curve in your drawing. Are you looking at the tangent vector to the curve? Or are you just looking at a general vector that lies in the submanifold?

It is written here to get rid of cross terms the tangent vectors $\frac{∂}{∂V^I}$ (here $\frac{∂}{∂r}$) is made perpendicular to the submanifolds.

Written where?

Can anyone please explain what is the last line trying to say

What last line are you talking about?

if we consider our 3-D space foliated by 2-sphere then the metric becomes...

Yes, this is correct.

our known metric is $dr^2+r^2d\Omega^2$

This is the known metric with a particular choice of coordinates. There are other possible coordinate choices.

how are these $f_1(r)$ and $f_2(r)$ are determined??

By choosing particular coordinates.

 

[Apashanka]

Tangent vector to what? You have drawn a curve in your drawing. Are you looking at the tangent vector to the curve? Or are you just looking at a general vector that lies in the submanifold?

Tangent vector to a curve

 

[PeterDonis]

Tangent vector to a curve

Then the tangent vector has to point along the curve. It doesn't look like it does in your drawing.

 

[Apashanka]

Written where?

https://www.google.com/url?sa=t&sou...FjACegQIBhAB&usg=AOvVaw1YY2mM7uccdbX4nTxFgQO5
Page -166 equation 7.2

 

[Apashanka]

Then the tangent vector has to point along the curve. It doesn't look like it does in your drawing.

Ya it is along $\hat \theta+\hat \phi$ ,coefficients apart

 

[Apashanka]

By choosing particular coordinates.

We have here chosen spherical polar coordinates for which $f_1=1$ and $f_2=r^2$, then how it is coming??

 

[PeterDonis]

It is written here to get rid of cross terms the tangent vectors $I\frac{∂}{∂V^I}$ (here $\frac{∂}{∂r}$) is made perpendicular to the submanifolds.

Page -166 equation 7.2

It doesn't say anywhere on that page that the tangent vectors $I\frac{∂}{∂V^I}$ are "made" perpendicular to the submanifolds. You don't have to "make" that be true. It automatically is true just from the foliation.

 

[PeterDonis]

Ya it is along $\hat \theta+\hat \phi$ ,coefficients apart

The tangent vector in your drawing is $T$. It doesn't look like $T$ is pointing along the curve. It looks like it's pointing perpendicular to the curve, which is wrong.

 

[PeterDonis]

We have here chosen spherical polar coordinates for which $f_1=1$ and $f_2=r^2$, then how it is coming??

Because you chose it.

 

[Apashanka]

It doesn't say anywhere on that page that the tangent vectors $I\frac{∂}{∂V^I}$ are "made" perpendicular to the submanifolds. You don't have to "make" that be true. It automatically is true just from the foliation.

In the second paragraph it is written that cross terms between $du^i$ and $dV^j$ are not present in the $ds^2$ as the tangent vector $\frac{∂}{∂V^I}$ are orthogonal to the submanifolds.(in 2nd paragraph).
That's what I am not understanding.

Could you please help me out
What tangent vector is $\frac{∂}{∂V^I}$ ??
For this 3-D space foliated by 2-sphere it is then $\frac{∂}{∂r}$ and metric $ds^2=f_1(r)dr^2+f_2(r)d\Omega^2$ (where $f_1=1$ and $f_2=r^2$ )assuming that $\frac{∂}{∂r}$ is orthogonal to the 2- sphere
Could you please explain it...

 

[Apashanka]

The tangent vector in your drawing is $T$. It doesn't look like $T$ is pointing along the curve. It looks like it's pointing perpendicular to the curve, which is wrong.

It should point along $\hat \theta+\hat \phi$,isn't it??
Sorry diagramatically it pretends to be pointing otherwise

 

[PeterDonis]

That's what I am not understanding.

What are you not understanding? Why the cross terms aren't there if the tangent vectors are orthogonal to the submanifolds?

 

[PeterDonis]

It should point along $\hat \theta+\hat \phi$,isn't it??

The tangent vector should point along the curve. That's what "tangent" means.

 

[Apashanka]

What are you not understanding? Why the cross terms aren't there if the tangent vectors are orthogonal to the submanifolds?

Yes what the tangent vector $\frac{∂}{∂V^I}$ is ??And how it's orthogonality to the submanifold omits the cross terms from the metric ??
Because till now we only know tangent vector to a curve whose component along the $\mu^{th}$ direction is $\frac{dx^\mu(\lambda)}{d\lambda}$

 

[PeterDonis]

Yes what the tangent vector $\frac{∂}{∂V^I}$ is ??

In your example, it's $\partial / \partial r$.

how it's orthogonality to the submanifold omits the cross terms from the metric ??

Orthogonality of two vectors $U^\mu$ and $V^\nu$ means that $g_{\mu \nu} U^\mu V^\nu = 0$. That means there can't be any components of $g_{\mu \nu}$ that have an index $\mu$ for which $U^\mu$ is not zero, and an index $\nu$ for which $V^\nu$ is not zero. So, for example, if $\partial / \partial r$ is going to be orthogonal to any vector that lies in the 2-sphere submanifold, then there can't be any cross terms in $g_{\mu \nu}$ where $\mu = r$ and $\nu = \theta$ or $\nu =\phi$.

 

[PeterDonis]

till now we only know tangent vector to a curve

So you just pick any curve that has all coordinates constant except the one you're interested in. So, for example, $\partial / \partial r$ is a tangent vector to any curve that has all coordinates constant except $r$.

 

[Apashanka]

So you just pick any curve that has all coordinates constant except the one you're interested in. So, for example, $\partial / \partial r$ is a tangent vector to any curve that has all coordinates constant except $r$.

Can we then say that the curve is parametrised by $r$ similar to what we are used of which is $\lambda$??

 

[Apashanka]

In your example, it's $\partial / \partial r$.
Orthogonality of two vectors $U^\mu$ and $V^\nu$ means that $g_{\mu \nu} U^\mu V^\nu = 0$. That means there can't be any components of $g_{\mu \nu}$ that have an index $\mu$ for which $U^\mu$ is not zero, and an index $\nu$ for which $V^\nu$ is not zero. So, for example, if $\partial / \partial r$ is going to be orthogonal to any vector that lies in the 2-sphere submanifold, then there can't be any cross terms in $g_{\mu \nu}$ where $\mu = r$ and $\nu = \theta$ or $\nu =\phi$.

It is therefore ($\frac{∂}{∂r}$ pointing along $\hat r$)??

 

[PeterDonis]

It is therefore ($\frac{∂}{∂r}$ pointing along $\hat r$)??

$\partial / \partial r$ is $\hat{r}$. They're two different notations for the same thing.

 

[George Jones]

$\partial / \partial r$ is $\hat{r}$. They're two different notations for the same thing.

By $\hat{r}$, @Apashanka might mean $\left| \hat{r} \right| = \left| g\left( \hat{r} , \hat{r}\right) \right| = 1$.

 

[pervect]

It is therefore ($\frac{∂}{∂r}$ pointing along $\hat r$)??

Yes, people have tried to mention this several times now by my reading of the thread.

Let us use the spherical line element
$$ds^2 = dr^2 + r^2 \,d\theta^2 + r^2 \sin^2 \theta \, d\phi^2$$

I can't make your diagram out well enough to figure out if this line element that I wrote corresponds to your diagram though :(.

With the above line element, $\frac{\partial}{\partial r} = \hat{r}$. However, $\frac{\partial}{\partial \theta} = r \hat{\theta}$. So in general it is not true that $\frac{\partial}{\partial x^i} = \hat{x^i}$, though they point in the same direction.

In the notation you appear to be used to, $\frac{\partial}{\partial x^i}$ always points in the same direction as $\hat{x^i}$, but $\frac{\partial}{\partial x^i}$ does not necessarily have a unit length. But $\hat{x^i}$ does have a unit length, by defintion. Thus we can say $\frac{\partial}{\partial x^i} = K \, \hat{x^i}$ where K is the length of $\frac{\partial}{\partial x^i}$.

For the line element I wrote, the length of $\frac{\partial}{\partial r}$ is 1, the length of $\frac{\partial}{\partial \theta}$ is r, and the length of $\frac{\partial}{\partial \phi} = r \, \sin \theta$

In general, given a metric $g_{ij}$ the length of $\frac{\partial}{\partial x^i}$ is $\sqrt{ | g_{ii} |}$. This follows from the fact that the length^2 of a vector with components $u^i$ is $g_{ij} u^i u^j$.

 

[Apashanka]

So you just pick any curve that has all coordinates constant except the one you're interested in. So, for example, $\partial / \partial r$ is a tangent vector to any curve that has all coordinates constant except $r$.

Okk if $\lambda$ is the parametrisation of the curve and all other coordinates remain constt. along the curve except $x^{jth}$
then at any $\lambda$ the tangent vector is $\frac{dx^{jth}}{d\lambda}\hat x^{jth}$
In spherical polar coordinate a straight line from the origin is an example where only r changes along the curve and (θ,Φ) remains constt.
So the tangent vector will be $\frac{dr}{dλ}\hat r$ throughout the curve.
If λ being the length along the curve then tangent vector is simply $\hat r$ throughout the curve.
How is then tangent vector becomes $\frac{∂}{∂r}$ as you said above??

 

[PeterDonis]

If λ being the length along the curve then tangent vector is simply $\hat r$ throughout the curve.
How is then tangent vector becomes $\frac{∂}{∂r}$ as you said above??

$\hat{r}$ and $\partial / \partial r$ are the same thing, as I said in post #21. So if the curve is purely in the $r$ direction, the tangent vector is $(dr / d\lambda) (\partial / \partial r)$. And if $\lambda$ is arc length along the curve, and the curve is purely in the $r$ direction, then $\lambda = r$, so $dr / d\lambda = 1$. So the tangent vector is just $\partial / \partial r$.

 

[PeroK]

Okk if $\lambda$ is the parametrisation of the curve and all other coordinates remain constt. along the curve except $x^{jth}$
then at any $\lambda$ the tangent vector is $\frac{dx^{jth}}{d\lambda}\hat x^{jth}$
In spherical polar coordinate a straight line from the origin is an example where only r changes along the curve and (θ,Φ) remains constt.
So the tangent vector will be $\frac{dr}{dλ}\hat r$ throughout the curve.
If λ being the length along the curve then tangent vector is simply $\hat r$ throughout the curve.
How is then tangent vector becomes $\frac{∂}{∂r}$ as you said above??

There's a correspondence between vectors and directional derivatives that can be formalised mathematically. This is an important mathematical element that you need to master.

I must admit it took me a good deal of effort to really understand the whole concept. Learning GR was the first time I'd come across it.