dexstarr
- 4
- 0
Hey Everyone,
I'm having trouble setting up this word problem.
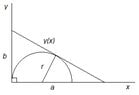
I know that area of a circle is pir2 and area of a triangle is 1/2bh but for some reason I can't find a way to combine these equation together.
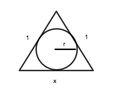
What are the radius and area of the circle of maximum area that can be inscribed in an isosceles triangle whose two equal sides have length 1?
I'm having trouble setting up this word problem.
I know that area of a circle is pir2 and area of a triangle is 1/2bh but for some reason I can't find a way to combine these equation together.
What are the radius and area of the circle of maximum area that can be inscribed in an isosceles triangle whose two equal sides have length 1?