Maximizing Cam Follower Mass for Contact with Rotating Cam: A Dynamic Analysis

[i_am_imbact]

Hello,
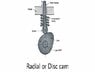
I have a problem in which I know the constant of the spring,the maximum and minimun force that the spring does to the camand the rotational speed of the cam.I am asked to find the necessary mass to attach to the spring in the follower so the follower always stays in contact with the cam.I am attaching the picture of the cam and the follower.Also we know that the Y(θ)=h/2(1-cos(θ) 0<θ<90 the follower goes up 90<θ<180 the follower goes down and on 180<θ<360 the follower is dwelling/

 

[BvU]

Hi,

Also we know that the Y(θ)=h/2(1-cos(θ)

Do we ? Looks more like the red guy:

And the most likely place to lose contact is at $\theta = 90^\circ$ where the spring has to accelerate maximum the whole lot: roller, washer, spring itself, roller follower and whatever it attached above.

[edit]although the amplitude is less: $y = 1-1/2\,\cos(2\theta)$ or so.

 

[i_am_imbact]

Hi,
Do we ? Looks more like the red guy:

View attachment 263201

And the most likely place to lose contact is at $\theta=906 \circ$ where the spring has to accelerate maximum the whole lot: roller, washer, springitself, roller follower and whatever it attached above.

Sorry I made I mistake I meant 1-cos(2θ) also we don't consider the roller , spring and washers have any mass,we only need to find a relation for the mass of the roller follower so the cam is always in touch with the roller.I though maybe if we make the ode of the roller follower and we demanded that the y(θ) is a solution we find the necessary mass

 

[BvU]

Zero is best

 

[jrmichler]

also we don't consider the roller , spring and washers have any mass,we only need to find a relation for the mass of the roller follower so the cam is always in touch with the roller

NO, NO, NO. You need to consider ALL of the moving mass driven by the cam. And your question makes sense if you are looking for the maximum mass for a certain speed of the cam.

The solution starts with a clear description of the system. In this case, start by making four plots. Each plot covers 360 degrees of cam rotation. One plot is cam follower position vs rotation angle, one plot is follower velocity vs rotation angle, the third plot is follower acceleration vs cam angle, and the fourth plot is spring force vs cam angle. The first two plots are not strictly necessary, but you should do them in order to better understand the system.

Then you use F = ma, where F is the spring force, m is the total cam follower moving mass, and a is the acceleration of the moving mass. When F = ma, the follower is losing contact with the cam. When F > ma, the follower stays in contact with the cam. When F < ma, the follower loses contact with the cam.

 

[i_am_imbact]

NO, NO, NO. You need to consider ALL of the moving mass driven by the cam. And your question makes sense if you are looking for the maximum mass for a certain speed of the cam.

The solution starts with a clear description of the system. In this case, start by making four plots. Each plot covers 360 degrees of cam rotation. One plot is cam follower position vs rotation angle, one plot is follower velocity vs rotation angle, the third plot is follower acceleration vs cam angle, and the fourth plot is spring force vs cam angle. The first two plots are not strictly necessary, but you should do them in order to better understand the system.

Then you use F = ma, where F is the spring force, m is the total cam follower moving mass, and a is the acceleration of the moving mass. When F = ma, the follower is losing contact with the cam. When F > ma, the follower stays in contact with the cam. When F < ma, the follower loses contact with the cam.

Thank you very much,
Also I would like to ask you if the possibility for the follower to lose contact with the cam only lies when the cam is going down.Also for example with a=a(θ) and F=-Kx , x=x(θ),in order to find the maximum mass we need to form the equation w(θ)=-K*x(θ)/x''(θ) and find the maximum for these equation between 90<θ<180?​