[Cam Design] Calculation of torque required by cam shaft

[kingneptune11]

Hello all,

I am trying to figure out how to calculate the torque on a cam shaft.

Say we are looking at this cam and cam follower:

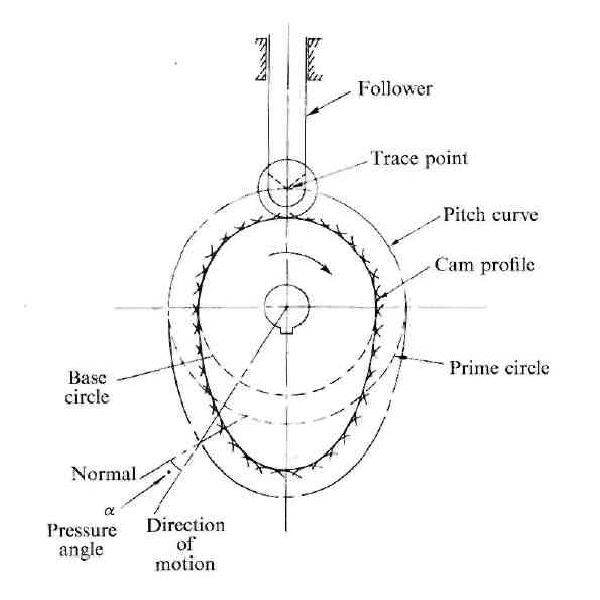
If we know that the total force downward caused by the cam follower is, let's say, 50lb, how do I determine the torque required of the cam shaft to rotate the cam at any given cam angle? I was under the impression it was the following:

Cam Shaft Torque = (Normal Force of cam follower on cam)(distance from cam shaft center to point of contact between cam and cam follower)(tan(pressure angle))

However, I am still confused about this. I cannot seem to find any cam design references online that discuss the calculations of the cam shaft torque. I can only find information regarding the velocity profiles of the cam. Can anyone help me with this? Or maybe can someone point me in the direction of some good online references that discuss this topic?

Thank you.

 

[haruspex]

From a little elementary geometry, I agree with the formula you quote. Are you just wanting confirmation, or a proof, or something else?

 

[vaidyanathan1102]

This may help you !
http://www.ijsr.net/archive/v2i6/IJSRON20131137.pdf

 

[Ranger Mike]

woha up there , pardner. 50 pounds down force is wayyyy low.
the following are for one valve spring.

Solid Flat Tappet Camshaft: 130 lbs Seat Pressure/300-325 lbs open pressure
Hydraulic Roller Camshaft: 130 lbs Seat Pressure/300- 325 lbs open pressure
Solid Roller Camshaft: (Minimum Safe Pressures)Up to .600? valve lift: 200-235 lbs Seat Pressure/600 lbs open pressure
Over .600? valve lift: 250-280 lbs Seat pressure /100 lbs pressure for every .100? of valve lift

consider this is the pressure it takes to open ONE VALVE. multiply this by 8 for a 4 cylinder engine. some designs have 4 valves per cylinder. you may want to rethink torque required to turn a bum stick.

 

[CWatters]

Old thread alert.

 

[Randy Beikmann]

Another way to approach it is to calculate the work in moving the follower, first using torque, and then using force. The two must be equal. So at any point in the motion,

T dtheta = F dx

Then T = F dx/dtheta

The term dx/dtheta is the "velocity" of the follower, relative to the cam rotation angle, and is easy to get. (You can also get actual velocity from v = (dx/dtheta) (dtheta/dt) = dx/dt.)

As for the force, it has two parts. First the spring force, which is simply k(x+x_seat), where x_seat is the deflection of the spring from its free length, when the valve is closed (the force is already large when leaving the seat). But don't forget the force from accelerating the follower and whatever it's pushing (mTotal)! In an automotive application, that would be the masses of the follower, the valve, and 1/3 of the spring. So this part of F is m_Total (d2x/dt^2). And d2x/dt^2 is just equal to (d2x/dtheta^2)(dtheta/dt)^2.

You'll get the same answer, but this is easier to me. You could also throw in the friction force, if you determine it's significant.

 

[jack action]

I know this is an old thread, but there is not a real answer for the problem.

Being lazy, I took the following image from here:

Assume the vertical distance $R_2$-$N\sin\phi$ is $L$ and the vertical distance $R_1$-$R_2$ is $d$.

Then we know the following (from $\sum F_y , \sum F_x, \sum M_{@R_2}$):

$N\cos\phi = F + \mu(R_1 + R_2)$
$N\sin\phi = R_2 - R_1$
$dR_1 = LN\sin\phi$

Where $F= ky + m\ddot{y}$, i.e the spring force and inertia reaction of the follower components.

Which leads to:

$N = \frac{ky + m\ddot{y}}{\cos\phi - \mu\left(2\frac{L}{d} + 1\right)\sin\phi}$

The instantaneous torque $T$ will be:

$T = ( A + Bf_r)N$

Where:

$A$ is the perpendicular distance between the normal force $N$ and the center of rotation;
$f_r$ is the rolling resistance coefficient of the roller;
$B$ is the perpendicular distance between the rolling resistance $f_rN$ and the center of rotation.
(Too lazy to mathematically define $A$ & $B$ )

It is interesting to note that $N=\infty$ when $1 = \mu\left(2\frac{L}{d} + 1\right)\tan\phi$ which is why there is a rule of thumb that says that $\phi < 30°$ to avoid excessive side load on the sliding follower.

 

[Rx7man]

It would be wise to remember that at low RPM, the forces are regenerative, and especially on multi cylinder engines, the cam really doesn't need much torque to turn.. HOWEVER, as you increase speed, especially approaching valve float RPM, this no longer happens, and you have to factor in the force for accelerating the valve, not just the spring pressure.

A simplified way of solving this would be to find the work required to open the valve and divide it by the time or angle required to do it in.. this would give a fairly close approximation of the average torque needed.. you can add work needed for friction and acceleration as well

 

[vaidyanathan1102]

Another way to approach it is to calculate the work in moving the follower, first using torque, and then using force. The two must be equal. So at any point in the motion,

T dtheta = F dx

Then T = F dx/dtheta

The term dx/dtheta is the "velocity" of the follower, relative to the cam rotation angle, and is easy to get. (You can also get actual velocity from v = (dx/dtheta) (dtheta/dt) = dx/dt.)

As for the force, it has two parts. First the spring force, which is simply k(x+x_seat), where x_seat is the deflection of the spring from its free length, when the valve is closed (the force is already large when leaving the seat). But don't forget the force from accelerating the follower and whatever it's pushing (mTotal)! In an automotive application, that would be the masses of the follower, the valve, and 1/3 of the spring. So this part of F is m_Total (d2x/dt^2). And d2x/dt^2 is just equal to (d2x/dtheta^2)(dtheta/dt)^2.

You'll get the same answer, but this is easier to me. You could also throw in the friction force, if you determine it's significant.

But the unit we get here for torque is Nm/s which is the unit for power right ? so its not the torque that we will get by solving the above formula right ?

 

[OldYat47]

In practical terms there are a number of things affecting the loading on an individual cam lobe.
- Spring pressure at any given point in the cycle
- The effect of horizontal offset between the roller (as pictured) center and the camshaft center of rotation
- Inertia of the tappet and anything it is moving (varies, of course, as the tappet lifts)
The above can be calculated
- Friction in the tappet and any other mechanical devices (like valves, for example) (this friction will vary with side loading)
And as mentioned above, you get some of the work back on the "downside" of the tappet stroke. Gotta remember that.