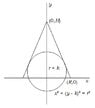
No...$h=r+k$, you need to find $a$ as I described (the positive $x$-intercept of the circle), and you need to find the constraint. The most straightforward way I can think of is to use the fact that a radius of the circle drawn to the point of tangency of the line segment from $(0,H)$ to $(R,0)$ is perpendicular to this segment, and so the formula for the perpendicular or shortest distance between a point and a ine may be used to obtain the value of $k$ in terms of $R$, $H$ and $r$. Another method which yields the same result, but requires more algebra is to equate the equation of the line to the circle and require the discriminant of the resulting quadratic to be zero.
The formula for the distance $d$ between a point $\left(x_0,y_0 \right)$ and a line $y=mx+b$ is:
$$d=\frac{\left|mx_0+b-y_0 \right|}{\sqrt{m^2+1}}$$
We know in this case that $d=r$. Can you identify $m$ and $b$?