Maximum Amplitude of a Function

[paulmdrdo]

I was able to find the maximum value for this function by differentiating and equating it to zero and find the time t and substitute it back to the original expression to get the max amplitude.

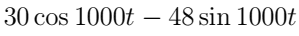
tm = -0.001012 s
v(tm) = 56.6
Another method that was presented in my book was

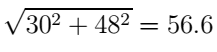can you explain how did the author came up with this solution? TIA.

(mentor note: moved from another forum to here --> hence no template)

 

[BvU]

Another method that was presented in my book

You want a repeat of what's in your book ? Or do you have a specific question about that presentation ?
Do you know how to deal with trigonometric equations like $a\cos x + b\sin x =c$ ?

[edit] since you apparently managed to solve

by differentiating and equating it to zero

I must assume you do ...

 

[mfb]

That is one of the results you derive once and then know. You can repeat what you did with general coefficients a and b and you'll get an amplitude of $\sqrt{a^2+b^2}$. Alternatively you can look up the formula to combine the sum of a cosine and a sine into a single sine (with a phase shift), the formula for the amplitude has what you are looking for. That formula is derived the same way.