Maxwell and The distribution of velocities in a gas

[Aleoa]

In the first volume of his lectures (cap 6-4) Feynman presents Maxwell's distribution of velocities of the molecules in a gas.

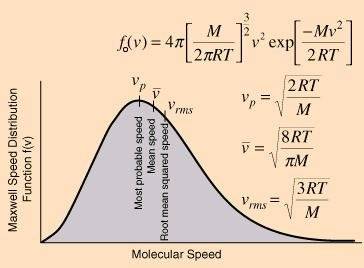And, referring to the PDF graph he says:

"If we consider the molecules in a typical container (with a volume of, say, one
liter), then there are a very large number N of molecules present (N ≈ $10^{22}$).
Since p(v) ∆v is the probability that one molecule will have its velocity in ∆v,
by our definition of probability we mean that the expected number <∆N> to be
found with a velocity in the interval ∆v is given by: $<\Delta N>=Np(v)\Delta v$.
[...]
Since with a gas we are usually dealing with large numbers of molecules,
we expect the deviations from the expected numbers to be small (like 1/√N), so
we often neglect to say the “expected” number"

I have not understand this part, how it's possible to derive this 1/√N deviation ( or a value the gives the idea of what Feynman is saying) ?
Thanks for your support

 

[willem2]

I have not understand this part, how it's possible to derive this 1/√N deviation ( or a value the gives the idea of what Feynman is saying) ?

This is the central limit theorem. If you have N identically distributed random variables with mean μ and variance σ², the average of the variables will approach a normal distribution for large N with mean μ and variance σ²/N. The standard deviation will be $\frac {\sigma}{\sqrt N}$. The average speed of the molecules is such a set of random variables, but you can also use a variable that is 1 if the speed is in a certain range, and 0 if it is not, and you can use this to calculate the standard deviation for the number of molecules in a certain velocity range,

 

[Aleoa]

This is the central limit theorem. If you have N identically distributed random variables with mean μ and variance σ², the average of the variables will approach a normal distribution for large N with mean μ and variance σ²/N. The standard deviation will be $\frac {\sigma}{\sqrt N}$. The average speed of the molecules is such a set of random variables, but you can also use a variable that is 1 if the speed is in a certain range, and 0 if it is not, and you can use this to calculate the standard deviation for the number of molecules in a certain velocity range,

I'm not able to understand which is , in this case, the average random variable that is subjected to CLT ...
How does the bold phrase in the main post concern to the distribution of sample mean ?

 

[mjc123]

I think there's a step missed out (assumed), and a slight error. If the probability of a single molecule having a velocity in the range v → v + Δv is p(v)Δv, then for N molecules, the number with a velocity in that range follows a binomial distribution, with a mean (expectation value) of Np(v)Δv and a variance of Np(v)Δv(1-p(v)Δv), which is approximately Np(v)Δv if p(v)Δv << 1. So the standard deviation is √(Np(v)Δv); note that this increases as √N (the error in the statement above). The fraction of molecules with velocities in the range Δv has an expectation value Np(v)Δv/N = p(v)Δv, and a standard deviation of √(p(v)Δv/N). This is the "deviation that goes like 1/√N".

 

[Stephen Tashi]

I'm not able to understand which is , in this case, the average random variable that is subjected to CLT ...

Assume each of $N$ particles has a independent probability of $p(v_1) dv$ of having (at a given time) its velocity in $I_1$ and probability of $1 - p(v_1)dv$ of having its velocity in some other interval. Whether a particle has a velocity in $I$ is a Bernoulli random variable with probability of success equal to $p(v_1)dv$.

The number of particles (at a given time) that have their velocities in $I_1$ is a binomial random variable $B_1$ . The random variable $B_1$ is the sum of $N$ identical independent Bernoulli random variables.

Feynman's remark says that (at a given time) the number of particles that have their velocities in $I_1$ has a high probability of being close to the mean of $B_1$, which is $N p(v_1) dv$.

There are some technicalities to consider.

1. Does "close" mean close in the absolute sense - e.g. within plus or minus 2? Or does "close" mean in the sense of a percentage - e.g. within plus or minus 2% of $N$?

2. The analysis for one interval $I_1$ is a not joint result about what happens for two different intervals $I_1,I_2$. Whether a particle has a velocity in $I_1$ is not independent of whether it has a velocity in $I_2$.
Feynman's claim is that (jointly) for each interval $I_j$ the number of particles with velocities in that interval has a high probability of being $Np(v_j) dv$.

Of course, physicists don't always worry about mathematical technicalities!