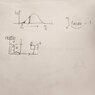'Residence' time distribution function for a Pulse input

[DumpmeAdrenaline]

Residence time distribution- the time an entering particle spends in a system before it leaves. The residence time of molecules in a system is measured using tracers. The response for a system is recorded for some type of perturbation.

Consider $$ A+B \rightarrow C $$ and suppose we want to know the residence time distribution of molecule A. We select tracer T with similar properties to A which is non-adsorbing and non-reacting.

Assume a constant density system.
Lets say we inject a quantity N0 of tracer molecules in an instantaneous injection. The way I am thinking of it is as if a clock is attached to each molecule from the N0. Once a molecule leaves, the clock displays the residence time and there is a tracker of the proportion of N0 that leave the system at the same residence time. We can express N/N0 as a frequency or cumulative frequency distribution.$$(t,\frac{N}{N_{0}}) $$. However, it is physically impossible to measure for each time in an interval the proportions of molecules and I am not sure if the data collected is continuous or discrete. Since, if we repeat the same experiment any number of times a different distribution will be produced each time due to the randomness of molecular interactions, so we mathematically model the frequency distribution using a normal distribution function called the density function, f(t). How to interpret f(t)? Can I think of f(t) as the rate of molecules leaving the reactor at time t per N0. By integrating, we obtain all the molecules that have left the reactor which must equal to N0/N0=1. This corresponds to the area under a probability function. The number of tracer molecules N0 and N are not measurable quantities we divide by the volume of the vessel to get concentration C and C0.

I don't understand how the mathematics leads to what we are trying to determine: the time that molecule A spends in the reactor and remains available to react with molecule B to form molecule C.

 

[hutchphd]

The number of tracer molecules N0 and N are not measurable quantities we divide by the volume of the vessel to get concentration C and C0.

What does this mean? You actually measure C and C0?

The central limit theorem is at work here

 

[DumpmeAdrenaline]

The number of tracer molecules cannot be measured directly under experimental conditions. Therefore, we divide by the volume of the vessel it is in to obtain measurable concentration quantities.

 

[hutchphd]

You divide "what" by the volume ("what" is something that you measure I presume?)
So you measure concentrations.....and infer numbers by multiplying by volume. I see now.
The Gaussian follows from the MVT mentioned above..read about this remarkably useful result.

 

[DumpmeAdrenaline]

After reviewing the CLT, I have realized that I have misinterpreted things. Instead of C(t)/C(t=0) the random variable of interest is the residence time t. According to the CLT, the distribution of the standardized sample residence time means approaches the standard normal distribution as the sample size approaches infinity. If I inject a fixed quantity N0 into the vessel and measure both the concentration and time. For each t I would measure C(t) and repeat this for many samples with a fixed injection of N0 then I would calculate mean from all the samples. $$ \frac{t(C(t_{1})+..C(t_{n}))}{nC(t=0)} $$ where t is fixed and C(t_{1}) is the concentration evaluated at t for sample 1 up t n. Repeat for different t we can measure form a distribution that distribution would be a standard normal. But I dont know the population mean residence time nor the variance of residence time.

 

[Chestermiller]

You have a chemical reactor of volume V with a feed stream having volumetric flow rate Q flowing through the reactor. What is the mean residence time in the reactor? You introduce a short tracer pulse of high molar concentration C* into the feed stream during the time interval $-\Delta t/2$ to $+\Delta t/2$, where $\Delta t$ is short. How much tracer have you introduced into the reactor (in moles) essentially at time zero? If the reactor is well-mixed, what is the concentration of tracer exiting the reactor as a function of time? What would the concentration vs time graph look like if the reactor were not well-mixed?

 

[DumpmeAdrenaline]

$$ \frac{V}{Q}- \hspace{0.1cm} \text{time required to fill a chemical reactor of volume V.}$$
$$ C^{*}\Delta{V}- \hspace{0.1cm} \text{Number of moles that are present in the differential volume of the feed stream over} \hspace{0.1cm} \Delta{t} $$$$ \frac{C^{*}\Delta{V}}{V}- \hspace{0.1cm} \text{Oulet concentration}$$
The concentration in a well-mixed reactor is uniform and spatially independent when the moles are instantaneously and uniformly distributed throughout the reactor. Therefore, the concentration at the outlet will be equal to the concentration within the reactor. As a result, the concentration versus time curve will look something like this. In the case of a non well-mixed reactor the moles are not distributed uniformly throughout the reactor.

 

[Chestermiller]

$$ \frac{V}{Q}- \hspace{0.1cm} \text{time required to fill a chemical reactor of volume V.}$$
$$ C^{*}\Delta{V}- \hspace{0.1cm} \text{Number of moles that are present in the differential volume of the feed stream over} \hspace{0.1cm} \Delta{t} $$$$ \frac{C^{*}\Delta{V}}{V}- \hspace{0.1cm} \text{Oulet concentration}$$

The volume of the reactor doesn't change. The number of moles of tracer entering the reactor is $C^*Q\Delta t$. Because the reactor is well mixed the initial concentration of tracer in the reactor is $$C_0=\frac{C^*Q\Delta t}{V}=\frac{M_0}{V}$$where $M_0=C^*Q\Delta t$

The concentration in a well-mixed reactor is uniform and spatially independent when the moles are instantaneously and uniformly distributed throughout the reactor. Therefore, the concentration at the outlet will be equal to the concentration within the reactor. As a result, the concentration versus time curve will look something like this. In the case of a non well-mixed reactor the moles are not distributed uniformly throughout the reactor.

Your result for a well-mixed reactor is incorrect. The concentration balance of tracer in the reactor should be $$V\frac{dC}{dt}=-QC$$ where the right hand side represents the rate at which tracer is leaving the reactor and the left hand side represents the rate of change of tracer within the reactor. The solution to this equation is $$\frac{C}{C_0}=e^{-\frac{Qt}{V}}$$. This is also equal to the mass of tracer remaining within the reactor at any time divided by the initial mass of tracer in the reactor.

At what value of t has half the mass of tracer exited the reactor? What is the fraction remaining in the reactor at the mean residence time t = V/Q?

What would the fraction of tracerremaining in the reactor vs time look like for a plug flow reactor (no mixing within reactor0?

 

[DumpmeAdrenaline]

Your result for a well-mixed reactor is incorrect. The concentration balance of tracer in the reactor should be $$V\frac{dC}{dt}=-QC$$ where the right hand side represents the rate at which tracer is leaving the reactor and the left hand side represents the rate of change of tracer within the reactor. The solution to this equation is $$\frac{C}{C_0}=e^{-\frac{Qt}{V}}$$. This is also equal to the mass of tracer remaining within the reactor at any time divided by the initial mass of tracer in the reactor.

To understand why my result for a well-mixed reactor is incorrect is it because the system in consideration is a control volume and thus the concentration of tracer will vary with time (more tracer molecules will leave as time progresses) and that we are injecting once. So, the rate at which the tracer is leaving the reactor depends on how much tracer there is in the reactor?At what value of t has half the mass of tracer exited the reactor? What is the fraction remaining in the reactor at the mean residence time t = V/Q?

$$ \frac{C}{C_{0}}=0.5=e^{-\frac{Qt}{V}} \rightarrow -ln(2)=-\frac{Qt}{V} \rightarrow t=\frac{ln(2)V}{Q} $$ 50% of the mass will leave the system at the above time.
At the mean residence time t=V/Q $$\frac{C}{C_{0}} \approx 0.367 $$ At the mean residence time t=V/Q 36.7% of the initial mass remains in the reactor.

Since a plug flow reactor can be modeled as a series of infinitely thin plugs with uniform composition traveling in the axial direction, with each plug having the same composition as the ones before and after it (because a tracer is a non-reactive species), the outlet response of the system would start at 0. By the time it reaches the end of the reactor length, the outlet would record a step up equal to the initial concentration.

 

[Chestermiller]

To understand why my result for a well-mixed reactor is incorrect is it because the system in consideration is a control volume and thus the concentration of tracer will vary with time (more tracer molecules will leave as time progresses) and that we are injecting once.

Not only that. After the initial tracer injection, the flow into the reactor is pure, and does not contain any tracer. So it acts to purge the tracer out of the reactor.

So, the rate at which the tracer is leaving the reactor depends on how much tracer there is in the reactor?

Yes.

At what value of t has half the mass of tracer exited the reactor? What is the fraction remaining in the reactor at the mean residence time t = V/Q?

$$ \frac{C}{C_{0}}=0.5=e^{-\frac{Qt}{V}} \rightarrow -ln(2)=-\frac{Qt}{V} \rightarrow t=\frac{ln(2)V}{Q} $$

This is 69.3% of the mean residence time.

50% of the mass will leave the system at the above time.
At the mean residence time t=V/Q $$\frac{C}{C_{0}} \approx 0.367 $$ At the mean residence time t=V/Q 36.7% of the initial mass remains in the reactor.

Since a plug flow reactor can be modeled as a series of infinitely thin plugs with uniform composition traveling in the axial direction, with each plug having the same composition as the ones before and after it (because a tracer is a non-reactive species), the outlet response of the system would start at 0. By the time it reaches the end of the reactor length, the outlet would record a step up equal to the initial concentration.

In other words, none of the mass comes out until the mean residence time. Immediately after, all the mass has exited.

Are you starting to get a feel for this now?

 

[DumpmeAdrenaline]

Not only that. After the initial tracer injection, the flow into the reactor is pure, and does not contain any tracer. So it acts to purge the tracer out of the reactor.

Do we call the flow almost pure because we are adding a small volume of a concentrated tracer?

In step input, how do we make an abrupt change in the concentration of the tracer? Is the only difference between a step input and a pulse input is the initial concentration of the tracer in the reactor. Cumulative and washout functions remain the same since they don''t depend on the initial concentration.

What confuses me is that we are supposed to use residence time theory to analyse non-ideal reactors when the assumptions of ideal reactors are no longer valid. Yet we still rely on the assumptions of ideal reactors. Above, we used the assumption of perfect mixing assumption (the concentration is spatially independent) to obtain the residence time distributions of a perfectly mixed CSTR and PFR.

 

[Chestermiller]

Do we call the flow almost pure because we are adding a small volume of a concentrated tracer?

No. After the pulse of tracer is added, we continue flowing the feed with no tracer contained in the feed.

In step input, how do we make an abrupt change in the concentration of the tracer? Is the only difference between a step input and a pulse input is the initial concentration of the tracer in the reactor. Cumulative and washout functions remain the same since they don''t depend on the initial concentration.

We have been flowing a feed stream containing tracer. At time zero we switch the feed stream to feed flow without dissolved tracer. Or, if we are flowing a feed stream without tracer, at time zero we switch to feed stream to feed flow with dissolved tracer. These are both versions of the step input.

What confuses me is that we are supposed to use residence time theory to analyse non-ideal reactors when the assumptions of ideal reactors are no longer valid. Yet we still rely on the assumptions of ideal reactors. Above, we used the assumption of perfect mixing assumption (the concentration is spatially independent) to obtain the residence time distributions of a perfectly mixed CSTR and PFR.

The perfectkt mixed reactor represents one limit, and the plug flow reactor represents the other limit. All real reactors perform between these two limits. We can simulate this real behavior by using perfectly mixed tanks in series. As we reduce the number of tanks to 1, we obtain a totally perfectly mixed reactor while if we increase the number of perfectly mixed tanks in series, each with a volume of V/n, we approach the residence time distribution of plug flow. So by doing a residence time distribution measurement on the actual reactor, we calibrate the number of tanks to be used to the experimental data. This will tell us how many tanks to use in an model simulation of the reactor with the kinetics included.

 

[DumpmeAdrenaline]

No. After the pulse of tracer is added, we continue flowing the feed with no tracer contained in the feed.

We have been flowing a feed stream containing tracer. At time zero we switch the feed stream to feed flow without dissolved tracer. Or, if we are flowing a feed stream without tracer, at time zero we switch to feed stream to feed flow with dissolved tracer. These are both versions of the step input.

The perfectkt mixed reactor represents one limit, and the plug flow reactor represents the other limit. All real reactors perform between these two limits. We can simulate this real behavior by using perfectly mixed tanks in series. As we reduce the number of tanks to 1, we obtain a totally perfectly mixed reactor while if we increase the number of perfectly mixed tanks in series, each with a volume of V/n, we approach the residence time distribution of plug flow. So by doing a residence time distribution measurement on the actual reactor, we calibrate the number of tanks to be used to the experimental data. This will tell us how many tanks to use in an model simulation of the reactor with the kinetics included.

I am not sure if this thought is correct for explaining why a perfectly mixed CSTR forms the upper limit for residence time distributions of all real reactors. It would take more time for an impeller to distribute uniformly the tracer molecules moving randomly throughout the reactor which are also at the same being discharged from the reactor and disturbing that uniformity.

For given reactor volume and flow rate as we increase the number of tanks in series we approach the residence time distribution of a plug flow reactor. This is because the concentration increases due to a fixed number of moles present in a decreasing volume. Consequently as we continue flowing the feed without a tracer the time the tracer spends in each reactor is negligible.

If we write the mole tracer balance for both a perfectly mixed CSTR of volume V and the first reactor in the series of CSTR reactor of volume V/n where n is the number of tanks approaching infinity. The exponential function decreases to 0 at a faster rate than the n approaching infinity in the nN0/V implying that the residence time of tracer in every reactor is negligible

$$ C(t)=\frac{N_{0}}{V} e^{-\frac{t}{t_m}} $$
$$ C(t)=\frac{n*N_{0}}{V} e^{-\frac{t*n}{t_m}} $$

 

[Chestermiller]

I am not sure if this thought is correct for explaining why a perfectly mixed CSTR forms the upper limit for residence time distributions of all real reactors.

It represents the broadest distribution of residence times.

It would take more time for an impeller to distribute uniformly the tracer molecules moving randomly throughout the reactor which are also at the same being discharged from the reactor and disturbing that uniformity.

Oh really? What if the impeller is rotating a zillion RPM and the feed rate to the reactor is I cc/year?

 

[DumpmeAdrenaline]

Hi Prof. Chester
I would like to gain a better understanding of the mathematical concepts of the density function, cumulative distribution function, and washout function in the context of studying the residence time distribution of tracer molecules in a vessel. Suppose we instantaneously inject a fixed amount of tracer molecules, N0, into the feed stream of a vessel at t=0, and we monitor the concentration of tracer at the outlet to track the proportion of molecules that have exited the vessel.

During the time interval [t, t+dt], the measured outlet concentration is C(t), and therefore the proportion of tracer molecules with residence time between t and t+dt is dN=QC(t)dt. We define the f(t) (the density function) such that f(t)dt=dN/N0 but why can't we define f(t)=dN/N0 is this incorrect because f(t) which is supposed to be time dependent will not be so because the dt in the RHS will cancel?

By integrating f(t) we are effectively summing up the proportion of tracer molecules that have exited the system. This sum corresponds to the cumulative distribution function F(t) (the area under f(t) vs t graph) which represents the proportion of tracer molecules with residence time between 0 and t. Further we define the washout function W(t) 1-F(t)=W(t) where W(t) can it be interpreted as the proportion of tracer molecules that remain in the reactor (whose residence time is greater than t).