janu203
- 35
- 2
For the Image given, i have to calculate reluctances of air gap and core which depends on respective mean path lengths.
For the left hand core, the mean path length calculated in the solution manual is 1.11 meter . However what I don't understand is that why is the length of the air gap included in calculating mean path length of the core?
Don't we have to subtract the air gap length from the core so that true mean path length of the left core can be calculated?
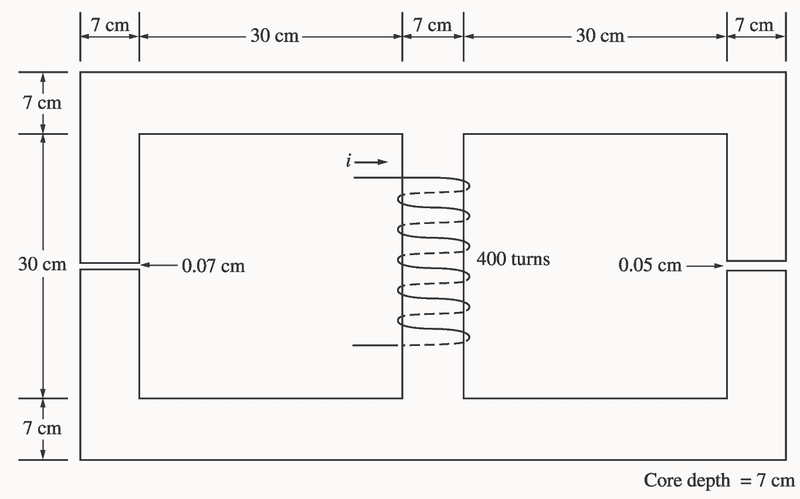
For the left hand core, the mean path length calculated in the solution manual is 1.11 meter . However what I don't understand is that why is the length of the air gap included in calculating mean path length of the core?
Don't we have to subtract the air gap length from the core so that true mean path length of the left core can be calculated?