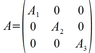Measure with a zero-energy fundamental state

[Keru]

Homework Statement

Given the following Hamiltonian:

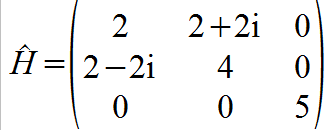
And the observable:

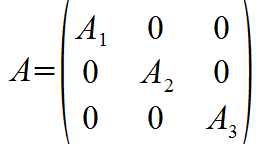
Calculate the probability of measuring any of the possible values of A in the fundamental state.

The attempt at a solution

I have calculated the eigenvectors and eigenvalues of the Hamiltonian, being the eigenvalues {0,5,6}
So the fundamental state have a zero energy. Is this relevant? Or has the same procedure as if the fundamental state was non-zero?
Also, how can I relate A and H? I'm very lost in Matrix Mechanics...

 

[kuruman]

I assume that by fundamental state you mean the state of lowest energy or ground state. No, the zero that you get is irrelevant. The reference zero point of energy is arbitrary. Here it happens that one of the states of the system is at zero. For the other question, you have the eigenvector corresponding to the ground state in a form that looks something like |V₁> = a₁|1> + a₂|2> + a₃|3>. What is the interpretation of the coefficients a_i?

 

[Keru]

I assume that by fundamental state you mean the state of lowest energy or ground state. No, the zero that you get is irrelevant. The reference zero point of energy is arbitrary. Here it happens that one of the states of the system is at zero. For the other question, you have the eigenvector corresponding to the ground state in a form that looks something like |V₁> = a₁|1> + a₂|2> + a₃|3>. What is the interpretation of the coefficients a_i?

Yes, i meant ground state. I translated it wrong from Spanish.
I know the chances of getting every possible measure are |a_i|², and that a_i = <V_i|V>. But I'm not sure what "V" is. I guess it must be a vector in order to get a scalar from the product, but what i (possibly wrongly) understand, is that V is a matrix containing the three possible eingenvectors... What am i missing?

 

[kuruman]

You got three eigenvectors when you diagonalized the Hamiltonian. Of these three choose the one that corresponds to eigenvalue zero. That's vector V.

 

[Keru]

You got three eigenvectors when you diagonalized the Hamiltonian. Of these three choose the one that corresponds to eigenvalue zero. That's vector V.

Wouldn't that be V_i?

 

[kuruman]

No it would not. It would be |V> which is a 3×1 column vector corresponding to eigenvalue zero. Can you show me what eigenvector you got for eigenvalue zero?

 

[Keru]

No it would not. It would be |V> which is a 3×1 column vector corresponding to eigenvalue zero. Can you show me what eigenvector you got for eigenvalue zero?

Sure.
$$ V_1= \frac {1} {\sqrt{3}} (-1 - i, 1, 0) $$

 

[kuruman]

Good. Now think of this as a vector written in unit vector notation as
$$|V_1>= \frac {(-1-i)} {\sqrt{3}}|1> + \frac {1} {\sqrt{3}}|2>+\frac {0} {\sqrt{3}}|3>$$
where $|1>,~|2>$ and $|3>$ are the unit vectors or more correctly the ordered orthonormal basis set. It is the basis in which A is diagonal, that is $<i|A|j>=A_i \delta_{ij}$. Note that you can also write $V_1$ in general as $$|V_1>= \sum_{k=1}^3a_k|k>$$
where $a_k=<k|V_1>$. Now go back and read your post #3. Do you see what's going on?

 

[Keru]

Ok, I finally got it. Had a confusion with the basis, but now i know what I was getting wrong. I'm still a newbie at QM, thanks for the patience and for the help, you have my sincere "like" !

(Thread can be closed now i guess)

 

[kuruman]

(Thread can be closed now i guess)

Actually, no. Others may choose to post their comments. However, as the OP you can click "Mark Solved" (upper right) if you wish.