Tone L
- 72
- 7
- TL;DR
- Building a simple instrument to effectively collimate sunlight and measure the digital counts on a photo detector.
Summary:
This is a hobbyist project I am working on. I am building an instrument to measure radiance from the sun at 500 nm, using optically filtered photodetector with bandwidth ± 10 nm. This type of science can be called Sun Photometry, so let's get to it!
Geometry for Optics:
The sun has an angular size of about .53 degrees, this is a simple calculation, angular size = arctan(d/D), where d is diameter of the sun and D is distance from the sun from Earth. With that being said, you would need an instrument with an angular field of view equal or larger than .53 degrees to view the disk of the sun.
However, due to homogeneity of our atmosphere and the resulting aural around the sun it has been stated in that an angular field of view of 2.5 degrees for instrumentation is best for sun photometry, approximately five times the angular size of the sun.
Design:
We need angular field of view to equal 2.5, so will have a collimating tube of 110 cm and an aperture of 5 mm assuming the detector is a point.
2.56 = arctan(5/110), painted black with 90% absorbance.
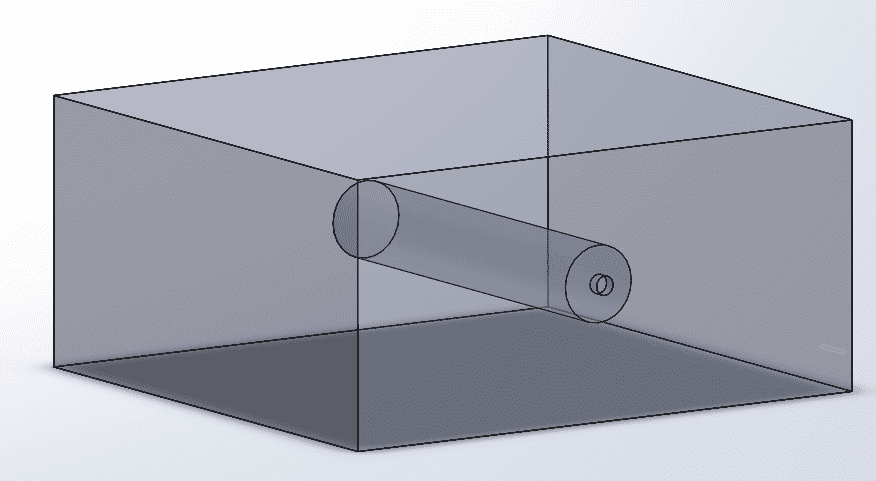
Here is a CAD of the optical block.
Where things go astray...
Simulation:
I was curious how much sunlight would enter the aperture and be collimated down to the "detector" (there is no detector in the model).
I tried to simulate the sun here by knowing that the ratio of the diameter to the distance (.0093 = diamter:distance) from Earth is about .0093. So at .1 meters away the size of the sun would be 930 microns.
Now using RayViz a package within Solidworks I made a disk, which is the "sun" here and I tried plotting the rays from the surface of this disk, and well doesn't look to great! Here I have a lambertian surface meaning the rays leave at all angles of the disk. I don't know how to only focus the rays within instruments domain but nonetheless I think I am doing something wrong, not with the software but my thinking...The suns light is diffused and focused more than a lambertian surface...
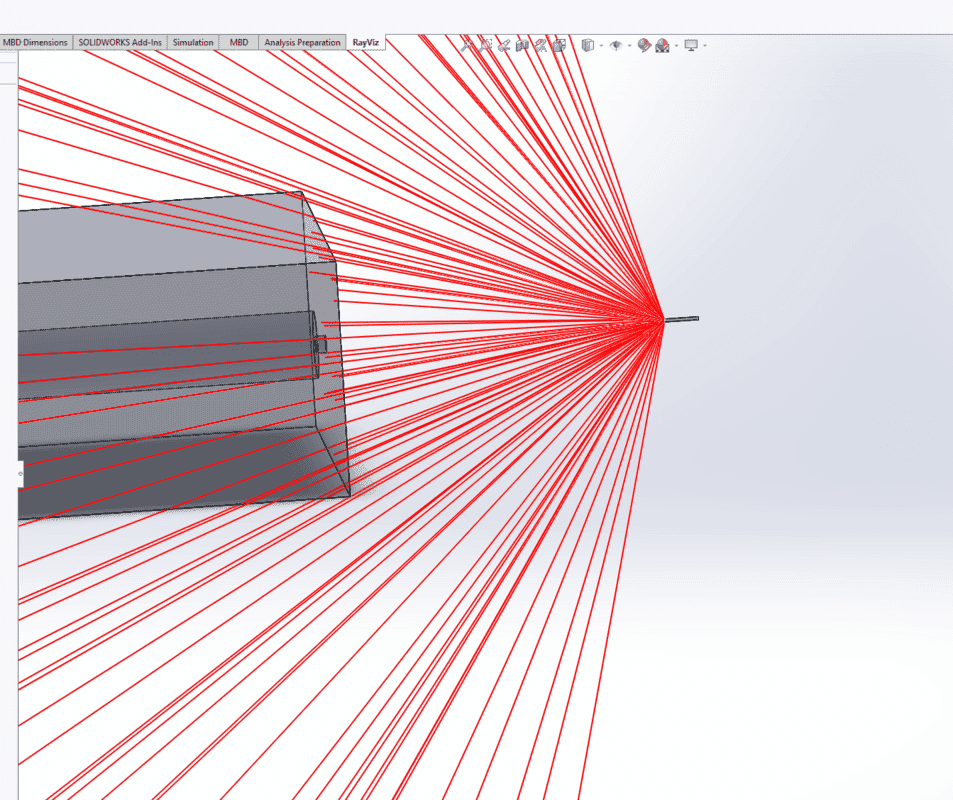
So, how would one simulate the sun, should it be a point source?
Cheers.
This is a hobbyist project I am working on. I am building an instrument to measure radiance from the sun at 500 nm, using optically filtered photodetector with bandwidth ± 10 nm. This type of science can be called Sun Photometry, so let's get to it!
Geometry for Optics:
The sun has an angular size of about .53 degrees, this is a simple calculation, angular size = arctan(d/D), where d is diameter of the sun and D is distance from the sun from Earth. With that being said, you would need an instrument with an angular field of view equal or larger than .53 degrees to view the disk of the sun.
However, due to homogeneity of our atmosphere and the resulting aural around the sun it has been stated in that an angular field of view of 2.5 degrees for instrumentation is best for sun photometry, approximately five times the angular size of the sun.
Design:
We need angular field of view to equal 2.5, so will have a collimating tube of 110 cm and an aperture of 5 mm assuming the detector is a point.
2.56 = arctan(5/110), painted black with 90% absorbance.
Here is a CAD of the optical block.
Where things go astray...
Simulation:
I was curious how much sunlight would enter the aperture and be collimated down to the "detector" (there is no detector in the model).
I tried to simulate the sun here by knowing that the ratio of the diameter to the distance (.0093 = diamter:distance) from Earth is about .0093. So at .1 meters away the size of the sun would be 930 microns.
Now using RayViz a package within Solidworks I made a disk, which is the "sun" here and I tried plotting the rays from the surface of this disk, and well doesn't look to great! Here I have a lambertian surface meaning the rays leave at all angles of the disk. I don't know how to only focus the rays within instruments domain but nonetheless I think I am doing something wrong, not with the software but my thinking...The suns light is diffused and focused more than a lambertian surface...
So, how would one simulate the sun, should it be a point source?
Cheers.
Last edited: