B Measuring Michelson–Morley light beams

[Ibix]

If I am correct, it will mean that me moving in space, and space moving past me is one and the same.

True.

However, if the Inferometer was not affected by Aether, will it be affected by its movement through space?

No. Why do I say that? You said it yourself (with two minor changes):

If I am correct, it will mean that methe interferometer moving in space, and space moving past methe interferometer is one and the same.

 

[P J Strydom]

There was no observed difference. Whether you include an "aether" or a "space" in the way you explain those observations is up to you. Einstein was able to do it without either. Why anyone would be interested in creating a more-complicated-than-necessary explanation seems to always be traced back to a prejudice about the way Nature ought to behave. It's apparently part of being human, because we've seen even the best of us do it.

Nature dictates how the light beams behave in the interferometer. Humans dictate how to explain the behavior. You cannot affect Nature's behavior by altering an explanation.

Naw, please note that I find these observations and calculations very interesting, and had huge difficuilties having it explained.
And as I said, I am not the cleverest peanut in the package.
And it is also not a situation where I am attempting to prove or disprove anything.

Look at what I achieved up to so far.
1. I was able to find out that.
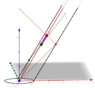
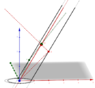
a beam traveling into supposed aether, and then with it upon return, will take longer on this round trip than a beam traveling perpendicular to this aether.
2. The distance the "horisontal beam" traveled, will stay the same, no matter how fast the inferometer travels through space, or through this aether.
The beam that traveled perpendicular to the direction of movement of the inferometer, will travel longer distances as speed increases.
3. However, the time the 2 beams will take to do their round trips, will be the same, no matter what speed it travels.
I hope my second and 3rd point of observation is correct.

Note: Now, by asking you simple questions, I learned things I never knew, no, I actually discovered it for myself as we went along.

The next thing that I am still confused about is:
...If the inferometer moves through space.
...the "Horizontal beam" travels at first with the direction of the Earths movement (for instance), then return against this movement.
...and the "Perpendicular beam" traveling across this movement (as we explained)
we know that the "Perpendicular beam" will travel a longer distance than the "Horizontal beam".

Q...(removing all notions of aether) is it true that there will be a difference in arrival times of the light beams, but due to the speed light travels at, it will be a difference of less than a 1% of a fringe, not noticeable by an inferometer?
MM did say he found a difference, but not what he expected.
if I may elaborate on how I came to this.
I took an Excel spreadsheet and entered the distance of MM's inferometer of 12 Meters, the speed of light, the speed of the Earth around its axis, and around the sun, and through space, and it shows that the perpendicular beam will be the retarded one, but by such a small amount, MM would not have seen it.

hey guys, I love this thing called relativity.
I hope I am not boring you all.

 

[Ibix]

Q...(removing all notions of aether) is it true that there will be a difference in arrival times of the light beams, but due to the speed light travels at, it will be a difference of less than a 1% of a fringe, not noticeable by an inferometer?

No. In an ideal experiment, analysed in a frame in which it is moving, both beams will return at the same time. If they do not then there is a way to detect absolute motion and therefore the principle of relativity should not be useful. But it is.

Real experiments do show fringe shifts due to things like temperature variation. Experimentalists control for this kind of thing as best they can, but inevitably there are imperfections. Michelson-Morley showed a slight sinusoidal variation of this type. They reported it, but note that it's not consistent with an ether model given the known speed of light. The kind of statistical analysis to estimate noise levels that is routine today wasn't done back then.

 

[Herman Trivilino]

The next thing that I am still confused about is:
...If the inferometer moves through space.

There is no experiment ever performed or observation made that can distinguish between a state of uniform motion and a state of rest. To say something moves through space is the same as saying it doesn't. A meaningless distinction.

Q...(removing all notions of aether) is it true that there will be a difference in arrival times of the light beams, but due to the speed light travels at, it will be a difference of less than a 1% of a fringe, not noticeable by an inferometer?

Every experiment or observation produces a result that may be off by a small but undetectable amount. But in the case of the MM experiment and its countless variations that amount is far less than 1%.

You do realize that a study of the MM experiment reveals how our ancestors came to their conclusions. Since that time so many more experiments have been performed and observations made that MM is just a drop in the bucket.

I took an Excel spreadsheet and entered the distance of MM's inferometer of 12 Meters, the speed of light, the speed of the Earth around its axis, and around the sun, and through space, and it shows that the perpendicular beam will be the retarded one, but by such a small amount, MM would not have seen it.

If you did it correctly any discrepancies must be due to round off error.

 

[P J Strydom]

No. In an ideal experiment, analysed in a frame in which it is moving, both beams will return at the same time. If they do not then there is a way to detect absolute motion and therefore the principle of relativity should not be useful. But it is.

Real experiments do show fringe shifts due to things like temperature variation. Experimentalists control for this kind of thing as best they can, but inevitably there are imperfections. Michelson-Morley showed a slight sinusoidal variation of this type. They reported it, but note that it's not consistent with an ether model given the known speed of light. The kind of statistical analysis to estimate noise levels that is routine today wasn't done back then.

Thanks.

 

[P J Strydom]

There is no experiment ever performed or observation made that can distinguish between a state of uniform motion and a state of rest. To say something moves through space is the same as saying it doesn't. A meaningless distinction.
Every experiment or observation produces a result that may be off by a small but undetectable amount. But in the case of the MM experiment and its countless variations that amount is far less than 1%.

You do realize that a study of the MM experiment reveals how our ancestors came to their conclusions. Since that time so many more experiments have been performed and observations made that MM is just a drop in the bucket.
If you did it correctly any discrepancies must be due to round off error.

This is why I am taking time to go through my thinking again.
The wonderful thing about the use of Excel, is that the fractions one can work with is immensely valued and eliminates any errors in calculations.

For instance, I took the values of c,
the speed of the Earth at 460 m/sec through space in the milky way,
and a length of an inferometer at 11 meters.

The beam traveling parallel to the Horizontal beam will arrive at
0.00000007333333334963 secs versus
0.00000007333333336593 secs.
in meters this is 0.00000000048889.
If I am correct, yellow light fringe is
0.00000054m
The light arriving later will have an effect of less than 0.905% of the sine wave of yellow light.
this will not show any interference.

This made me wonder about the observations.
1. that the parallel beam will travel slower, when clearly the perpendicular beam travels a longer distance.
2. that in relation to the Earths' axis, or even the position of the Earth around the Sun in 6 months will yield a minute result about measuring the position of the Earth, and the speed it travels at.

But as this may mean nothing, it is just some interesting knowledge I love thinking about.

The next thing that bothers me about the MM experiment is that all the physicists I know of, even Neil de grase Tyson, continuously state that due to the MM experiment, Einstein developed the theory of Special and General relativity.
So far, to me, they do not connect.
I will later on post what I don't understand, and perhaps you guys can explain it practical mechanics of this statement.

prosperous new year to you all.
May you guys get a flash of thought, and publish one heck of a paper.

 

[jbriggs444]

the speed of the Earth at 460 m/sec through space in the milky way

Yes, the rotation of the Earth on its axis produces a motion of plus or minus 460 meters per second depending on whether you sample at noon or midnight. But that is just the tip of the iceberg.

The orbital motion of the Earth about the sun is plus or minus 30,000 meters per second depending on whether you sample during summer or winter. But that again is small potatoes.

The orbital motion of the Solar system within the Milky way is 230,000 meters per second.

Until you have a test theory in mind to compare with the predictions of Special Relativity, you will not know which of these velocities, if any, is relevant. If, for instance, the test theory included a non-rotating ether which is dragged along with the Earth in its orbit about the sun then the expectation for a fringe shift corresponding to the Earth's 460 m/s rotational velocity would be correct. But other experiments rule out such a theory.

 

[Ibix]

The wonderful thing about the use of Excel, is that the fractions one can work with is immensely valued and eliminates any errors in calculations.

I hope you are joking. I don't think Excel goes beyond single precision. And I've found circumstances where it'll tell you that two values are equal, but if you subtract one from the other the answer isn't zero (probably an effect of it trying not to scare business users with the details of finite precision arithmetic in binary). Excel is one giant rounding error waiting to happen.

This is almost certainly why you have different answers for the travel time along the two paths - different cumulative rounding errors from different calculation orders. It's trivial to show algebraically that the difference is zero assuming the Lorentz transforms. If you get a different answer you must be making a mistake.

 

[jbriggs444]

I hope you are joking. I don't think Excel goes beyond single precision.

I just created a cell containing =1.0000000000001 + 1.0000000000001 and set the display format to 20 decimal places. The result displays as: 2.00000000000020000000

It looks to me like at least double precision. Wiki confirms.

"Excel calculates in double-precision floating-point format from the IEEE 754 specification[1] (besides numbers, Excel uses a few other data types[2]). Although Excel can display 30 decimal places, its precision for a specified number is confined to 15 significant figures, and calculations may have an accuracy that is even less due to three issues: round off,[3] truncation, and binary storage."

Edit: I found a more definitive test case...

The neatly rounded off decimal 2.000000000000020000000 did not smell right. That is not the result that one would naively expect from a double precision implementation. There had to be something more going on. And there is.

=sqrt(2) with a 20 digit display format yields 1.41421356237310000000
The correct result is 1.4142135623730950488016887242097

What Excel appears to do is to round displayed results at 14 sig figs even when the display format is set wider than that. Since double precision is good to 15 digits, this will [often] yield the expected result and will suppress meaningless trailing digits that might otherwise be inserted.

Even more interesting is the following spreadsheet containing:

=sqrt(2)             =a1*a1
=1.4142135623731     =a2*a2

Which displays as

1.41421356237310000000 2.00000000000000000000
1.41421356237310000000 2.00000000000001000000

 

[Ibix]

It looks to me like at least double precision. Wiki confirms.

"Excel calculates in double-precision floating-point format from the IEEE 754 specification[1] (besides numbers, Excel uses a few other data types[2]). Although Excel can display 30 decimal places, its precision for a specified number is confined to 15 significant figures, and calculations may have an accuracy that is even less due to three issues: round off,[3] truncation, and binary storage."

Ok - I'm over-estimating its awfulness. I've been bitten by being forced to use it as a semi-serious analytical tool too many times to trust it.

Since the differences seem to be arising on the 10th significant figure, I'm still betting on rounding error.

 

[vanhees71]

Well, according to Einstein himself, it's a fairy tail that he came to his special theory of relativity by thinking about the Michelson-Morley experiment. Indeed, when reading his famous 1905 paper "On electrodynamics of moving bodies", nothing the like is mentioned but a much more important way of thought was brought forward: The aim of writing this paper was to understand apparent asymmetries in the theory of electromagnetic phenomena (Einstein brings the example of a moving magnet inducing a current in a conducting loop at rest vs. the same situation in the reference frame, where the magnet is at rest and the loop moving). Of course, famously his solution was a revision of the very foundation of physics in terms of the description of space and time, introducing de facto the notion of "space-time".

The great genius of Einstein was to derive this revision of the space-time structure using the most simple facts of Maxwell's theory of electromagnetism together with the special principle of relativity, namely that if the special principle holds, then the speed of light in vacuo must be independent of the light-sources motion relative to any inertial observer. Indeed, as we know now, the only two space-time models consistent with the special theory of relativity and the usual symmetry assumptions ("Euclidicity" (homogeneity and isotropy) of space relative to any inertial observer as well as time-translation invariance of the natural laws for any inertial observer) leads to only two possible space-time models, namely the Galilean and the Minkowskian space-time manifolds. Only the latter involves a fundamental "limiting speed", which as far as we know today is the speed of light (i.e., the phase velocity of electromagnetic waves).

 

[P J Strydom]

Amaizing.! (The accuracy of excel)
This now forces me to go an work it out manually by hand.
I also made a practical drawing, measuring a theoretical moving diagram

The blue lines show the distance traveled perpendicular to movement of the Earth, and the red lines the parallel movement.
The first circle shows the initial departing positions, the second the point of reflection, and the 3rd the point of return to the splitter beam.
I simply increased the distance between the circles imitating an increase in speed
I copied the lines and changed the angles to horizontal, placed both lines next to each other, and measured the distance between the parallell lines and the angular lines.
I then moved the outer circles further away, thereby imitating an increase in speed, and did the measurements again, a few times.
What I found is that the return distance for the horizontal lines remains the same. But, the lines perpendicular increases in length as speed increases.
Now, this is highly exaggerated (to the effect of about 50% and 75% the speed of light), and if we were to use c as c, and v as 460 Km/sec, the difference will be very small, especially if we measure the distance of the light beams traveling over 11 Meters, as the MM inferometer.

I am sure that there must be a difference between the 2 beams arrival times.
Simply because one beam is traveling further.

 

[P J Strydom]

special principle holds, then the speed of light in vacuo must be independent of the light-sources motion relative to any inertial observer.

This makes absolute sense.
So, if a beam of light gets shot from a moving body, the speed of c will remain at c, and not c+v.
This will also mean, and this is the crucial point which is stuck in my head, that we will be able to detect if something is actually moving in relation to a fired light beam.
If we detect a red, or blue shift, it will mean that the object firing the light is either moving away from us, or advancing towards us.
Does this mean that if we fire a pulse of light in space, the light beam will spread out in a 3D ball, in relation to its point of origin?
this whilst the source of the light moves on?
Thinking of it this way opens another thought in my mind.
We will be able to detect which object is moving in relation to another, if both fires a pulse of light.
The one standing still, will not detect a fringe shift, whilst the object moving will.

Is this not what we see if we look at distant stars?
If we can see a red shift from a far off star, we must be able to see a shift in light on our inferometer.
it will however be very small indeed.
It is exactly the same as the 3 circle diagram I drew.
Anyhow,
lets get back to the "Audi" circle diagram.
Am I correct to say that the angular beam will travel a longer distance, than the horizontal one?
How big is the difference?

 

[vanhees71]

The redshift of stars is of course due to both relative motion to us and (for far distant ones) the gravitational Hubble-Lemaitre redshift. For this you need GR of course.

 

[Ibix]

I am sure that there must be a difference between the 2 beams arrival times.
Simply because one beam is traveling further.

You forgot about length contraction - the circles should be length contracted into ellipses. Please remember that relativity has been thoroughly picked over by literally thousands of people over the last century, and thoroughly tested. Any mistakes are your own.

Let the length of the transverse arm be $l$, and let the velocity of the apparatus be $v$. The time, $t_\bot$, for a pulse to return in this arm can be found by applying Pythagoras' theorem to the outbound path (or the inbound path, since both take the same time $t_\bot/2$):$$(ct_\bot/2)^2=(vt_\bot/2)^2+l^2$$This solves easily to give$$t_\bot=\frac{2l}{\sqrt{c^2-v^2}}=\frac{2l}{c\gamma}$$

Let the parallel arm have length $L$. The travel time in the outbound direction is $t_o$ and satisfies $ct_o=L+vt_o$, which gives $t_o=L/(c-v)$. The time in the inbound direction is $t_i$ and satisfies $ct_i=L-vt_i$, which gives $t_i=L/(c+v)$. The total time, $t_\parallel$, is the sum of these two. A little bit of algebra gives$$t_\parallel=\frac{2Lc}{c^2-v^2}=\frac{2L}{c\gamma^2}$$

So the two return times, $t_\bot=2l/c\gamma$ and $t_\parallel=2L/c\gamma^2$, are equal if $L=l/\gamma$ - i.e. if the parallel arm is length contracted in accordance with relativity.

 

[vanhees71]

For a very nice discussion of the MM experiment using the full SRT (also in frames, where the apparatus is moving!) to analyse the null result, see

https://doi.org/10.1119/1.17535

 

[Ibix]

We will be able to detect which object is moving in relation to another, if both fires a pulse of light.
The one standing still, will not detect a fringe shift, whilst the object moving will.

Are you describing three objects, two emitting pulses and the third receiving them? If so, yes, this is essentially how Doppler radar works. Or are you describing two objects exchanging pulses? In that case, both will see the other's pulse Doppler shifted.

 

[P J Strydom]

Ibex,
I agree with it all.
But keep in mind that I am not so intelligent as you scientists are.
To me something must be a mechanical entity.
What I mean by that is simply that one can look at any machine, and the rules of its design will dictate the outcome of what it is supposed to do.
A can opener will need its shortened blade to perce the lid, a fulcrum and lever, and energy to move the lever to cut the lid open.
The corkscrew was designed to remove a corkscrew.

Now, I can go and use Newtons' calculations to show that it is possible to open the can,
or I can take a can and open it.

Now, if I go through the calculations of Lorenz and I will determine the time and length of specific entities.
But why can I not simply draw the unit on paper, and measure what MM saw?

I am always feeling as if I am told, shutup and look at the maths.
I took a lot of time and I did the maths.
I agree with the maths, no question.

Then I went and look at why my logical mechanical explanation don't add up.
The only difference I find is the following.

1. Length contraction! Time dilation!.

What we all proved is that there will be a difference in the arrival of the light beams, but it will be such a negligent effect, that it is almost immeasurable.
We know there are a difference, but we will write it off with an explanation of length contraction.

And this is what I want to know...is length contraction and time dilation a theory, or experimental fact.
If fact, how do we prove with experiment that length contracts

 

[Ibix]

What we all proved is that there will be a difference in the arrival of the light beams, but it will be such a negligent effect, that it is almost immeasurable.

No. We've proved there is no effect. Without length contraction there would be an effect that would be easily within the detection range of Michelson and Morley's experiment.

And this is what I want to know...is length contraction and time dilation a theory, or experimental fact.

Time dilation has been directly observed many times - see cosmic ray muons, Hafele-Keating experiment, and pretty much every experiment run at CERN. Whether or not length contraction has been observed is a matter of opinion. We can't explain hordes of experiments without it (Michelson-Morley, any experiment in electromagnetism), and it's clearly implied by the invariance of lightspeed, which is also thoroughly tested. So I'd describe it as an experimental fact. But we've never literally photographed two rods side by side while one moved fast enough for length contraction to be visible.

But why can I not simply draw the unit on paper, and measure what MM saw?

Because you neglect effects like length contraction. So you are not modelling the world as it is. You would need to draw a Minkowski diagram to show the effects.

I am always feeling as if I am told, shutup and look at the maths.

The maths accurately describes the real world. It enables us to make precise numerical predictions that can be compared to the outcomes of experiments. And an accurate diagram expresses that maths somehow. Your "Audi" diagram is expressing a Newton+ether model, which is why it gives results consistent with that. If you shorten the parallel arm in accordance with relativity then you are expressing a relativistic model and you'll get a relativistic answer.

It won't tell you why lengthn contraction happens. I'd suggest you learn how to draw Minkowski diagrams for that.

 

[jbriggs444]

Does this mean that if we fire a pulse of light in space, the light beam will spread out in a 3D ball, in relation to its point of origin?
this whilst the source of the light moves on?

Not a 3-D ball. A spherical shell that expands over time.

Surprisingly, the invariance of light speed means that we can adopt the frame of reference where the source is at rest and observe an expanding spherical shell always centered on the source. It also means that we can adopt a frame of reference where the source is moving and observe an expanding spherical shell always centered on the place where the source was when it emitted the pulse. Both descriptions are correct!

The resolution to this seeming contradiction is the relativity of simultaneity. Each spherical shell is a snapshot at an particular instant in time. But time and, in particular, simultaneity, is judged differently from different reference frames.

 

[robphy]

Here's something that might be helpful.

https://www.geogebra.org/m/XFXzXGTq "Relativity-LightClock-MichelsonMorley-2018 (robphy)"

It's based on an old paper of mine
"Visualizing proper-time in Special Relativity" https://arxiv.org/abs/physics/0505134
and an old visualization (from http://visualrelativity.com/LIGHTCONE/LightClock/ )
that's now on youtube


With no length contraction, the Galilean-expected time-difference can, in principle, be measured by a very precise wristwatch.
But instead an optical interference experiment was used by MIchelson and Morley.
https://history.aip.org/exhibits/einstein/ae20.htm

 

[P J Strydom]

Not a 3-D ball. A spherical shell that expands over time.

Surprisingly, the invariance of light speed means that we can adopt the frame of reference where the source is at rest and observe an expanding spherical shell always centered on the source. It also means that we can adopt a frame of reference where the source is moving and observe an expanding spherical shell always centered on the place where the source was when it emitted the pulse. Both descriptions are correct!

The resolution to this seeming contradiction is the relativity of simultaneity. Each spherical shell is a snapshot at an particular instant in time. But time and, in particular, simultaneity, is judged differently from different reference frames.

Thanks, this is the first time someone said it in a way I understand.
if my terminologies are sounding funny, it is because I am not English, but well said.
What I like about your explanation is that you describe these expanding shells that is a snapshot in time.
these spheres of lifgt will obviously be as round as round can be, because the source of the light's velocity will have no effect upon it.

 

[P J Strydom]

Here's something that might be helpful.

https://www.geogebra.org/m/XFXzXGTq "Relativity-LightClock-MichelsonMorley-2018 (robphy)"
View attachment 236725View attachment 236726

It's based on an old paper of mine
"Visualizing proper-time in Special Relativity" https://arxiv.org/abs/physics/0505134
and an old visualization (from http://visualrelativity.com/LIGHTCONE/LightClock/ )
that's now on youtube


With no length contraction, the Galilean-expected time-difference can, in principle, be measured by a very precise wristwatch.
But instead an optical interference experiment was used by MIchelson and Morley.
https://history.aip.org/exhibits/einstein/ae20.htm

I will take the time an read everything over this weekend.
Much appreciated.

 

[Ibix]

I will take the time an read everything over this weekend.
Much appreciated.

Worth noting that these are the Minkowski diagrams I was recommending you learn about.

 

[Herman Trivilino]

Amaizing.! (The accuracy of excel)
This now forces me to go an work it out manually by hand.

Most of the Excel issues are probably due to the fact that the machine does its arithmetic in base 2. Try choosing values of $\frac{v}{c}$ that are powers of two.

 

[P J Strydom]

Whilst I am busy with the "Homework",
Can anyone explain in the simplest forms how Lorenz transformation lead to SR and GR?
I have difficulty understanding what the guys try to tell on You tube.
They contradict each other in many ways.

let me summarize how I understand it.
1. MM could not detect aether.
2. they thought a beam traveling in the direction of the aether will arrive later than one traveling across the aether.
3. They found the beams arrived at the same time.
4. but, Lorenz came forward with the length contraction calculation which says that anything moving against aether will undergo length contraction?
5. now, what does he say, there must be aether and everything squashes into itself as it travels against aether? (Confusion no 1)
6. then Einstein, and co came up with the Special relativity theory.
7. they say, as we travel in a direction, and we pulse a light beam forward and perpendicular to the direction of movement, the light beam that will reflect (in our time clock) from the ceiling, and the light beam that reflects from the front of our space ship, will arrive at the same time.
8. the beam that traveled to the ceiling, will travel a longer distance, but time will slow down for this beam, and it will arrive at the ceiling at the exact time the other beam reaches the nose.
9. upon these 2 beams return, the beam traveling from the ceiling will again travel further than the one from the nose, but time will again slow down for the beam from the ceiling, and both beams will arrive at the same time again.
lets stop here for now.
is this correct so far?

 

[vanhees71]

Here are my 2cts in trying to explain Special Relativity:

https://th.physik.uni-frankfurt.de/~hees/pf-faq/srt.pdf

 

[Ibix]

let me summarize how I understand it.

1-5 is more or less correct, except it's Lorentz. Lorenz was a different mathematician and physicist active at around the same time.

Lorentz and Fitzgerald proposed length contraction for no reason other than it explained the null result of Michelson-Morley. Lorentz later proposed the Lorentz transforms to fix the problems with Maxwell's equations which had started this whole line of investigation. But he just saw them as a patch to Maxwell's maths, for use in electromagnetism only.

Einstein showed independently that the Lorentz transforms arise from the principle of relativity and the constancy of the speed of light. He realized that they applied to everything and that, therefore, Newtonian physics was an approximation that is only valid at low speeds.

Unfortunately special relativity completely breaks Newtonian gravity. Because there's no propagation speed in Newtonian gravity it allows instant communication. But relativity says that "instant" is nonsense - different frames don't agree on what it means.

Minkowski pointed out that the Lorentz transforms were equivalent to the statement that space and time are part of a 4d entity we call spacetime. Einstein and others eventually realized that gravity could be explained by taking the flat spacetime and letting it curve.

Note that Michelson and Morley only appears in this as an inspiration for Lorentz-Fitzgerald contraction, which in turn is inspiration for the Lorentz transforms. Einstein was interested in the latter and their ability to solve problems with electromagnetism. Although the experiment is explained by relativity, it wasn't Einstein's motivation.

Applying the full Lorentz transforms doesn't make any difference to the analysis of the Michelson-Morley experiment. As long as you remember length contraction in the frame where the interferometer is moving the analysis can be done in either frame without worrying about the transforms.

 

[Ibix]

8. the beam that traveled to the ceiling, will travel a longer distance, but time will slow down for this beam, and it will arrive at the ceiling at the exact time the other beam reaches the nose.

No. Both beams travel the same distance. You do not need time dilation to understand the Michelson-Morley experiment. And the reflection events do not happen simultaneously except in the rest frame of the interferometer.

 

[Herman Trivilino]

7. they say, as we travel in a direction, and we pulse a light beam forward and perpendicular to the direction of movement, the light beam that will reflect (in our time clock) from the ceiling, and the light beam that reflects from the front of our space ship, will arrive at the same time.

The phrase "travel in a direction", or indeed just the word "travel" implies that there is something else involved, because there must be something that you're traveling relative to. An observer at rest relative to that something will indeed see both pulses leave at the same time and arrive at the same time. But that observer will see those pulses move further distances and therefore take more time.

Note that we are comparing what's observed by two different observers. We are not comparing the travel times of two different pulses measured by one of the observers.

8. the beam that traveled to the ceiling, will travel a longer distance, but time will slow down for this beam, and it will arrive at the ceiling at the exact time the other beam reaches the nose.

To either observer both beams take the same amount of time. The observers disagree on the amount of that time.