Michelson & Morley in Space-Time Diagram: Can't Make it Work

[Trysse]

TL;DR Summary

I thought it should be possible to draw a Minkowski space-time diagram that shows the light paths within the Michelson and Morley experiment.
https://en.wikipedia.org/wiki/Michelson%E2%80%93Morley_experiment
However, I am not able to make it work. So I wonder what is wrong with the diagram.

I have tried to draw a simplified diagram depicting the original Michelson experiment. I am only looking at the paths from the beam splitter to the mirrors at the end of the arms and back,

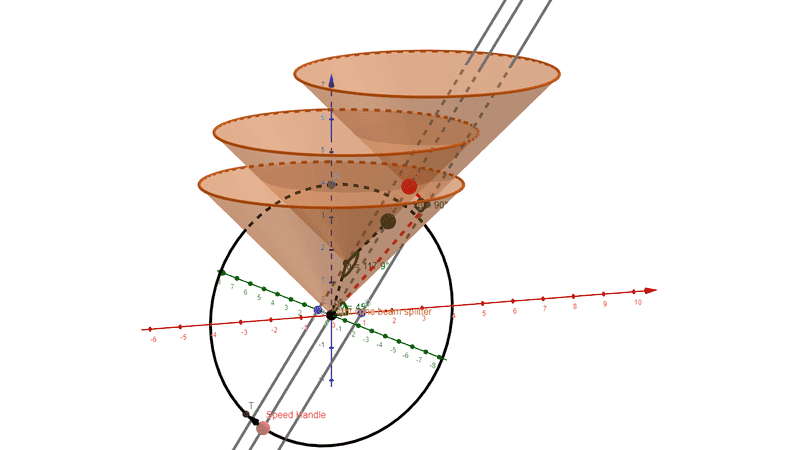
Below, you can see the following: A space-time diagram with two space axes (x andy) and one time axis (z).
There are three world lines: One going through the origin representing the position of the beam splitter (labeled b in the above picture). And two world lines representing the mirrors at the end of the arms (i.e. c and d in the above picture). These world lines go through the points (1,0,0) and (0,1,0).

I have three light cones: The bottom light cone depicts the event when the light is split at the beam splitter. The other two light cones "start" where the world lines of the mirrors intersect with the bottom light cone. These events are the reflection of the split signal at the mirrors. These two light cones include the signals returning from the mirrors to the beam splitter. At the points, where the world-line of the beam splitter intersects with these two light cones, are the fat red and black points. These points show where the light signal returns to the beam splitter.

Before I started to draw, I expected that the two endpoints of the light paths should coincide in one space-time event. However, as you can see they don't.

So this is my question:
Why is the diagram not showing the expected results, i.e. that both light paths end in one single event?
What adjustments are necessary to make the diagram work?

You can look at the original GeoGebra diagram here: https://www.geogebra.org/classic/mvxawhdx
To accelerate the system, move the red point at the bottom labeled "speed handle" to tilt the world lines of the system.

 

[vanhees71]

Well, you need a three-dimensional Minkowski diagram to depict time and the two directions of the light beams within the interferometer, as you show in your geogebra graphics. I must admit, I couldn't read off anything from such a Minowski diagram either.

The algebraic relativistic treatment in terms of four-vector transformations is not trivial either, but it's not as impossible as depicting it in Minkowski diagrams. You just start with the description in the interferometer's rest frame and Lorentz boost the result to a frame where it is moving. You'll find that the light paths are not perpendicular anymore as in the interferometer restframe but the aberration of the reflected light beams compensates this to get the null result found in experiment. This shows how the law of reflection looks for a moving mirror, and of course as anything concerned with Maxwell's equations (including optics) it's all fully Poincare covariant.

 

[robphy]

Before I started to draw, I expected that the two endpoints of the light paths should coincide in one space-time event. However, as you can see they don't.

So this is my question:
Why is the diagram not showing the expected results, i.e. that both light paths end in one single event?
What adjustments are necessary to make the diagram work?

View attachment 294466

You can look at the original GeoGebra diagram here: https://www.geogebra.org/classic/mvxawhdx
To accelerate the system, move the red point at the bottom labeled "speed handle" to tilt the world lines of the system.

Nice.

By the way, you're not really "accelerating" the system ... you are setting the velocity of the apparatus.

• The reason that the reception events do not coincide is that
  your apparatus does not feature length contraction.
  Your longitudinal arm's worldline always meets the event $(x,y,t)=(1,0,0)$.
  
  The signal along the longitudinal arm takes too long (compared to that of the transverse arm)
  to return to the moving source. The longitudinal arm is too far away for the receptions to coincide.
  Hence you have a velocity-dependent time-difference between receptions.
  
  Since this time-difference was too small to measure directly,
  an optical method using interference was used... hence the "interferometer".
  
  So, this setup of the arms is the expected behavior of Michelson-Morley apparatus
  according to pre-Special Relativity.
• To have the reception events coincide (as suggested by the results of the experiment),
  length contraction of the longitudinal arm is needed.
  Your longitudinal arm's worldline should meet the event $(x,y,t)=(1/\gamma,0,0)$,
  where $\gamma=\frac{1}{\sqrt{1-(v/c)^2}}$.
  
  
  
  Consult my Michelson Morley visualization with GeoGebra
  
  Relativity-LightClock-MichelsonMorley-2018 (robphy)
  https://www.geogebra.org/m/XFXzXGTq
  (I see
  https://www.geogebra.org/classic/XFXzXGTq
  gives an interface similar to yours.)
  
  UPDATE: Here is an old paper of mine, where I work out some of the geometry
  [already treated in typical textbooks] on a spacetime diagram
  "Visualizing proper-time in Special Relativity"
  https://arxiv.org/abs/physics/0505134

(By the way, when asking people to help debug a program,
it's good to show the program code.
I happen to know how to open the Algebra window in GeoGebra,
but many others may not.)

 

[Ibix]

Obviously something's wrong because the reflected rays should return to the beam splitter simultaneously in all frames if they do so in the rest frame, but it's impossible to say what you've actually done (Edit: unless you know more about Geogebra than I do, as @robphy apparently does).

If I were you, I'd extract the coordinates of the reflection and arrival events for a couple of speeds and crank out the correct answers by hand. Then you can see which, if either, of your rays is correct.

 

[vanhees71]

Nice.

By the way, you're not really "accelerating" the system ... you are setting the velocity of the apparatus.

• The reason that the reception events do not coincide is that
  your apparatus does not feature length contraction.
  Your longitudinal arm's worldline always meets the event $(x,y,t)=(1,0,0)$.
  
  The signal along the longitudinal arm takes too long (compared to that of the transverse arm)
  to return to the moving source. The longitudinal arm is too far away for the receptions to coincide.
  Hence you have a velocity-dependent time-difference between receptions.
  
  Since this time-difference was too small to measure directly,
  an optical method using interference was used... hence the "interferometer".
  
  So, this setup of the arms is the expected behavior of Michelson-Morley apparatus
  according to pre-Special Relativity.
• To have the reception events coincide (as suggested by the results of the experiment),
  length contraction of the longitudinal arm is needed.
  Your longitudinal arm's worldline should meet the event $(x,y,t)=(1/\gamma,0,0)$,
  where $\gamma=\frac{1}{\sqrt{1-(v/c)^2}}$.
  
  
  
  Consult my Michelson Morley visualization with GeoGebra
  
  Relativity-LightClock-MichelsonMorley-2018 (robphy)
  https://www.geogebra.org/m/XFXzXGTq
  (I see
  https://www.geogebra.org/classic/XFXzXGTq
  gives an interface similar to yours.)

(By the way, when asking people to help debug a program,
it's good to show the program code.
I happen to know how to open the Algebra window in GeoGebra,
but many others may not.)

I prefer to use Minkowski diagrams only for 1D motion, because already in 2D motion, where I need to draw 3 axes, I can't see much anymore anyway, how to depict full 4D is totally out of my imagination; algebra and analysis is a much simpler and better understandable way anyway; the ideal textbook on geometry has no pictures, like Euclid's elements.

Anyway, if you draw a Minkowski diagram for 1D motion you put first two axes (one for $x^0=ct$ and one for the direction the body is moving in, $x^1=x$) of the frame of reference, where the situation is most easily described. In this diagram you put the events (world lines of particles, world tubes of extended objects, the light cones originating in events, where you send out light signals,...). Then you draw two new axes for the boosted observer and construct the appropriate units of length by drawing the corresponding time- and space-like hyperbolae $(x^0)^2-x^2=\pm L^2$. Then you can read off what's going on in the new frame of reference.

As I said above, for 2D motion, I don't see much merit in drawing a Minkowski diagram.

 

[robphy]

I prefer to use Minkowski diagrams only for 1D motion, because already in 2D motion, where I need to draw 3 axes, I can't see much anymore anyway, how to depict full 4D is totally out of my imagination; algebra and analysis is a much simpler and better understandable way anyway; the ideal textbook on geometry has no pictures, like Euclid's elements.

..snip..

As I said above, for 2D motion, I don't see much merit in drawing a Minkowski diagram.

As the saying goes, "different strokes for different folks."

I'm a multimedia-type of person.
I strive to find different ways to express and emphasize ideas.
Sometimes this connects with analogous methods I already know.
Sometimes algebraic-calculation is needed. Sometimes geometric construction is needed.
Sometimes both... and sometimes neither.

I can't expect my audience to be comfortable with a certain way of thinking...
so I try to have other ways. (And maybe some other ways lead to other methods of calculation, like my causal-diamond approach!)
And I take pleasure when I can mesh different ways... arguably, greater than the sum of its parts.

In relativity, there is much said about the "geometry of spacetime".
It's sad to see the typical textbook emphasis on "transformation formula".
Do we teach and develop Euclidean geometry to beginners with rotation matrices and dot-products?
(N. David Mermin, Lapses in relativistic pedagogy, American Journal of Physics 62, 11 (1994); https://doi.org/10.1119/1.17728 )

While axiomatics, formalism, and formulas are good for some things,
visualization is good for other things.

While (1+1)-Minkowski diagrams are good for most typical textbook problems,
we need (2+1) or higher for other problems like the
analysis of the Michelson Morley experiment, or even the LIGO interferometer.
We also have real-world problems involving relativistic collisions (Compton effect), Thomas precession,
velocity-composition involving the transverse direction, the transverse Doppler effect,
and numerous situations involving the electromagnetic field
(for example, for many years, I've had a side project to visualize this calculation:
https://www.physicsforums.com/insig...rver-a-relativistic-calculation-with-tensors/ using differential forms on a spacetime diagram.)
...
not to mention relativistic optics and visual appearance in special relativity
and orbits in the Schwarzschild spacetime.

But, as I said, different strokes for different folks.

(Based on a question I had long ago...
From what I gather, Einstein did not reason with spacetime diagrams.
JL Synge did... by the way, there are view few spacetime diagrams of the Michelson Morley experiment.
Here is the only one I found, p. 158 from Synge's "Relativity: The Special Theory".)

 

[vanhees71]

As the saying goes, "different strokes for different folks."

I'm a multimedia-type of person.
I strive to find different ways to express and emphasize ideas.
Sometimes this connects with analogous methods I already know.
Sometimes algebraic-calculation is needed. Sometimes geometric construction is needed.
Sometimes both... and sometimes neither.

Ok, then just draw a Minkowski diagram for a particle moving in a circle in 2D (much simpler 2D motion than to draw a diagram for the Michelson Morley interferometer with the various "light rays" in it), that gives any insight into the geometry as seen in different ISs. I'm not against drawing Minkowski diagrams, where they really provide insight, although you have to put a lot of effort in explaining them to beginners in SRT: They must forget the Euclidean intuition they've built over their entire life as students from elementary school to the point studying SRT.

I can't expect my audience to be comfortable with a certain way of thinking...
so I try to have other ways. (And maybe some other ways lead to other methods of calculation, like my causal-diamond approach!)
And I take pleasure when I can mesh different ways... arguably, greater than the sum of its parts.

In relativity, there is much said about the "geometry of spacetime".
It's sad to see the typical textbook emphasis on "transformation formula".
Do we teach and develop Euclidean geometry to beginners with rotation matrices and dot-products?
(N. David Mermin, Lapses in relativistic pedagogy, American Journal of Physics 62, 11 (1994); https://doi.org/10.1119/1.17728 )

Well, of course we teach Euclidean geometry to beginners in math, i.e., starting in elementary school. There of course you cannot use the analytic approach to begin with. It's, however, good to use the analytic approach at the level of experience of the students when they start learning about SRT, which is after they have learned about Newtonian mechanics, which thank god (or rather Euler, Lagrange, Laplace, et al) we don't teach in the geometric way Newton wrote down his Principia anymore. That's for a very good reason!

While axiomatics, formalism, and formulas are good for some things,
visualization is good for other things.

I agree, of course. But a 3D Minkowski diagram is more confusing than illuminating the issue.

While (1+1)-Minkowski diagrams are good for most typical textbook problems,
we need (2+1) or higher for other problems like the
analysis of the Michelson Morley experiment, or even the LIGO interferometer.
We also have real-world problems involving relativistic collisions (Compton effect), Thomas precession,
velocity-composition involving the transverse direction, the transverse Doppler effect,
and numerous situations involving the electromagnetic field
(for example, for many years, I've had a side project to visualize this calculation:
https://www.physicsforums.com/insig...rver-a-relativistic-calculation-with-tensors/ using differential forms on a spacetime diagram.)

Hm, where is the spacetime diagram in this (very nice!) insights article, and if there was one, what would it help with the understanding of the transformation properties of the electromagnetic field? The formulae are pretty straight forward for themselves, aren't they?

...
not to mention relativistic optics and visual appearance in special relativity
and orbits in the Schwarzschild spacetime.

But, as I said, different strokes for different folks.

That's another thing. To simulate what I see in SR or GR, i.e., in a 3D space of an observer in a given state of motion against the observed objects (like a star or galaxy through a gravitational lense due to a Schwarzschild or Kerr black hole) seems to make much more things than to draw (1+2)-dimensional Minkowski diagrams.

(Based on a question I had long ago...
From what I gather, Einstein did not reason with spacetime diagrams.
JL Synge did... by the way, there are view few spacetime diagrams of the Michelson Morley experiment.
Here is the only one I found, p. 158 from Synge's "Relativity: The Special Theory".)

View attachment 294485

I don't have a clue what Synge has drawn there. I'd need more context (and maybe the formulae to understand what's drawn ;-)).

But as you say, maybe other people find such diagrams useful. I've nothing against them, as long as they are correctly interpreted, particularly there must be considerable emphasis (and even more considerable effort by the student) to forget Euclidean thinking when looking at a Minkowski space-time diagram (even in the simple (1+1)D case).

 

[robphy]

Possibly off-topic from the spacetime diagram for the Michelson-Morley apparatus,

(on the insight https://www.physicsforums.com/insig...rver-a-relativistic-calculation-with-tensors/ )
Hm, where is the spacetime diagram in this (very nice!) insights article, and if there was one, what would it help with the understanding of the transformation properties of the electromagnetic field? The formulae are pretty straight forward for themselves, aren't they?

When you teach electromagnetism, do you just use formulas
or do you also draw diagrams of vector fields (possibly with field lines)?

Is there some intuition gained from visualizing the pattern of the vector fields?
(I think there is some intuition from looking at the formulas as well as diagrams.)

As we have geometric constructions of kinematic situations
to describe transformation between frames,
we should have similar constructions for the electromagnetic field.

Following the idea that electromagnetism is already in accord with special relativity
(unlike kinematics which was forced to be revised), I would like to
think that methods of Minkowski spacetime geometry should be able to
handle electromagnetism. After all, the electromagnetic field is essentially a
two-form in spacetime (or pair of antisymmetric tensors related by Hodge-duality).
So, what is the geometric construction to take the pattern of field lines for E and B in one frame
and obtain the patterns in the other?
(My intuition tells me I need to focus on the spacetime differential forms, then spatial differential forms associated with an observer 4-velocity, and the spatial vector fields later (by use of the metric [By the way, I have a geometric construction for that]).)

This will require a Minkowski diagram in (3+1)-spacetime,
with certain aspects visible in (2+1)-diagrams... but maybe not so well in (1+1)-diagrams.

We now have easier access to visualization tools to do geometric constructions in more than 2 dimensions
and explore them interactively and dynamically.
So, for those who wish to try, why not try?

 

[Ibix]

I do think one needs to be very careful with the design of (2+1)d Minkowski diagrams, at least until I get my free-floating holographic display . I found the diagram in the OP a bit too busy - it's difficult to see what's going on with all the light cones, and some faint/dotted lines projecting events of interest onto axes would be helpful, IMO.

 

[vanhees71]

Possibly off-topic from the spacetime diagram for the Michelson-Morley apparatus,
When you teach electromagnetism, do you just use formulas
or do you also draw diagrams of vector fields (possibly with field lines)?

Is there some intuition gained from visualizing the pattern of the vector fields?
(I think there is some intuition from looking at the formulas as well as diagrams.)

As we have geometric constructions of kinematic situations
to describe transformation between frames,
we should have similar constructions for the electromagnetic field.

Following the idea that electromagnetism is already in accord with special relativity
(unlike kinematics which was forced to be revised), I would like to
think that methods of Minkowski spacetime geometry should be able to
handle electromagnetism. After all, the electromagnetic field is essentially a
two-form in spacetime (or pair of antisymmetric tensors related by Hodge-duality).
So, what is the geometric construction to take the pattern of field lines for E and B in one frame
and obtain the patterns in the other?
(My intuition tells me I need to focus on the spacetime differential forms, then spatial differential forms associated with an observer 4-velocity, and the spatial vector fields later (by use of the metric [By the way, I have a geometric construction for that]).)

This will require a Minkowski diagram in (3+1)-spacetime,
with certain aspects visible in (2+1)-diagrams... but maybe not so well in (1+1)-diagrams.

We now have easier access to visualization tools to do geometric constructions in more than 2 dimensions
and explore them interactively and dynamically.
So, for those who wish to try, why not try?

Of course I visualize vector fields with field lines and/or little arrows along them, if I think it's helping to understand the situation better, but that are of course not Minkowski diagrams but field pictures in 3D Euclidean space depicting the electric and magnetic 3D vector fields for an inertial observer. I've never seen Minkowski diagrams depicting the electromagnetic field. As you say that's very challenging since you'd need 4D (i.e., (1+3)D) Minkowski diagrams to begin with and somehow an intuitive picture for 2nd-rank antisymmetric tensors (or alternating two-forms) in Minkowksi space.

I've only never seen a (2+1)D Minkowski diagram I had some additional understanding from compared to the algebraic/analytic expressions. To visualize (3+1)D (i.e., four-dimensional) diagrams is completely out of my imagination (even the drawings of 4D Euclidean cubes you find in some books, don't help me in my intuition of 4D spaces), but of course it may be that other people gain something from such visualizations. As I said, I have nothing against such visualizations as long as they make a complicated mathematical subject more clear, but if they are more complicated to explain than the algebraic notation, I don't see too much merit in them.

 

[vanhees71]

I do think one needs to be very careful with the design of (2+1)d Minkowski diagrams, at least until I get my free-floating holographic display . I found the diagram in the OP a bit too busy - it's difficult to see what's going on with all the light cones, and some faint/dotted lines projecting events of interest onto axes would be helpful, IMO.

Indeed, that's the problem I also see with such an attempt.

 

[robphy]

I do think one needs to be very careful with the design of (2+1)d Minkowski diagrams, at least until I get my free-floating holographic display . I found the diagram in the OP a bit too busy - it's difficult to see what's going on with all the light cones, and some faint/dotted lines projecting events of interest onto axes would be helpful, IMO.

This is true with any visualization.
Often, I find that the limitations are due to the platform, which the designer must work around.

But of course it more important to sort out the physics first, then utility second, then appearance and interactivity.

 

[Ibix]

This is true with any visualization.

Sure. But 3d diagrams, particularly with transparent surfaces, is where I think it becomes difficult to design diagrams well. I've certainly seen 2d diagrams that are badly thought out (e.g. drawing a coordinate grid for every frame under the sun so the whole thing is a mass of lines), but 3d is where I think people come unstuck - partly from limitations of the tools, as you say.

A maxim we were given at work was that a diagram should use the absolute minimum amount of ink possible. Anything you don't need to make your point you should delete. As with all such general rules it's not completely true, but I've found it a useful guide. Applying it to the diagram in the OP is why I would have hidden the light cones, but dropped perpendiculars to the x-y plane and shown that the light paths were null by showing that the x-y extent equalled the t extent. No idea how easy that is to do in Geogebra, though.

But of course it more important to sort out the physics first, then utility second, then appearance and interactivity.

Definitely.

 

[vanhees71]

This is true with any visualization.
Often, I find that the limitations are due to the platform, which the designer must work around.

But of course it more important to sort out the physics first, then utility second, then appearance and interactivity.

I think geogebra is indeed a pretty convenient tool for analytical geometry and vizualization. It works nice for (1+1)D Minkowski diagrams too.

 

[vanhees71]

Sure. But 3d diagrams, particularly with transparent surfaces, is where I think it becomes difficult to design diagrams well. I've certainly seen 2d diagrams that are badly thought out (e.g. drawing a coordinate grid for every frame under the sun so the whole thing is a mass of lines), but 3d is where I think people come unstuck - partly from limitations of the tools, as you say.

Indeed, that's what I figured out too. The grid lines in (1+1)D Minkowski diagrams don't help (at least my) students to understand them better. Rather one should draw only the points, world lines, world tubes, etc. of interest together with the axes of the reference frames under consideration (maybe with tickmarks for the unit "lengths"), and if comparison of "lengths" are needed the corresponding hyperbolae to compare "spacetime distances" in different frames.

A maxim we were given at work was that a diagram should use the absolute minimum amount of ink possible. Anything you don't need to make your point you should delete. As with all such general rules it's not completely true, but I've found it a useful guide. Applying it to the diagram in the OP is why I would have hidden the light cones, but dropped perpendiculars to the x-y plane and shown that the light paths were null by showing that the x-y extent equalled the t extent. No idea how easy that is to do in Geogebra, though.

Definitely.

Hm, but for the Michelson-Morley experiment the light cones are crucial, aren't they?

geogebra is a great tool also for Minkowski diagrams, but as you say, (1+2)D diagrams are not very illuminating (at least not to me), and (1+3)D ones completely out of imagination.

 

[Ibix]

Hm, but for the Michelson-Morley experiment the light cones are crucial, aren't they?

Sure, and I assume OP has found the reflection events by intersecting the mirror lines and the cones. But do you need to display the whole cone? Isn't the worldline of the light along each arm (plus its projection on the t axis and the xy plane) enough?

 

[vanhees71]

I think so.

 

[Trysse]

@robphy Thanks a lot. Your hint that I must consider the length contraction on the arm in the direction of movement. I was somehow thinking that all effects such as the length contraction (and time dilation) spring automatically from the diagram. However, I missed that this is different when I consider a moving object in a stationary frame of reference.
Your example also gave me some ideas of what I can improve in using GeoGebra. Thanks for both.

@vanhees71 and @Ibix Thanks also for your consideration. The point of my question was really: What was wrong with my diagram in terms of construction. I agree with you that a 2+1 Monkowski diagram especially with the full cones is not easy "to see through". However, this exercise was for me personally to prove/see, that the Minkowski diagram can be used to depict the M&M experiment. Before going 2+1 I had tried to depict the experiment in a 1+1 Minkowski diagram but that did not work.

I found the reflection points on the world lines using the cones and when I worked on the diagram, I switched the cones on and of because they were in the way. I think for demonstration purposes @robphy 's diagram is better, where you can switch on and off the cones using a button and more transparency.

I think the 2+1 representation of the M&M experiment is a good way to show, what happens to objects that move through space. In a 1+1 diagram, it does not become as obvious, that objects flatten.

The correction of my error has been my personal epiphany regarding length contraction. From all the barn-and-pole and train-and-tunnel examples I never quite got it. Now I think I have understood and I imagine how objects become shorter as they move faster. Before I was still thinking, that the length contraction was an effect resulting from perspective and signal delay.

 

[vanhees71]

It's always the "relativity of simultaneity" which solves all these apparent paradoxes. I think the only merit of discussing all these paradoxes is to hammer this in your mind. Otherwise there's much more interesting physics in relativity than these pretty boring kinematic effects ;-)).