Measuring Pressure on a Concrete Table

[Kevin Cheung]

Homework Statement

To find the pressure difference between two points on the same surface

Relevant Equations

P=F/A

Hi guys, I am not doing homework, it is just suddenly brainstormed this question.

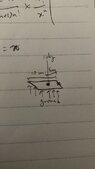
What if I place a very small mass like 10kg on the center of a concrete 10m*10m flat table supported by the ground, then how to measure the surface pressure acting on the center and right on the edge? Or the pressure difference between two particular points?

Pressure(center)=(10*9.8)/(?)
Pressure(edge)=(10*9.8)/(10*10)

It should be not correct, but how to measure the pressure at the particular point?

 

[phinds]

... how to measure the surface pressure acting on the center and right on the edge?

Draw a force diagram showing exactly what you have in mind.

 

[Kevin Cheung]

Draw a force diagram showing exactly what you have in mind.

It is just very simple, we can imagine it is not a "table" but a square solid.

 

[Gordianus]

What is the contact area between the mass and the table?

 

[Kevin Cheung]

What is the contact area between the mass and the table?

That is the tricky point, the weight is just like a point source, we could only have the information of dimension (the center to edge, the size of the table).

 

[phinds]

That is the tricky point, the weight is just like a point source, we could only have the information of dimension (the center to edge, the size of the table).

If the table is rigid, it really doesn't matter whether the force is a point source or spread evenly across the whole area, now does it?

 

[jbriggs444]

how to measure the pressure at the particular point?

The pressure of the ball at any point where the ball is not making contact is zero.

The pressure of an ideal ball on an ideal surface at the one and only point where contact is made would be infinite.

 

[Kevin Cheung]

The pressure of the ball at any point where the ball is not making contact is zero.

The pressure of an ideal ball on an ideal surface at the one and only point where contact is made would be infinite.

I get the point of the pressure of the contact point would be large as infinite, but could we tell the pressure difference between the contact point and the point away from it?

 

[phinds]

I get the point of the pressure of the contact point would be large as infinite, but could we tell the pressure difference between the contact point and the point away from it?

Do you know of any materials that could withstand infinite pressure?

 

[Kevin Cheung]

If the table is rigid, it really doesn't matter whether the force is a point source or spread evenly across the whole area, now does it?

Yes, assume it is rigid. I thought there are the same pressure on the two points before, but it seems wrong after considering the force is acting like a point.

 

[Kevin Cheung]

Do you know of any materials that could withstand infinite pressure?

No, so it should only be very high pressure.

 

[haruspex]

It is just very simple, we can imagine it is not a "table" but a square solid.

I'm unsure what you are asking. If you mean the distribution of the pressure the square exerts on the ground below it, it depends on the moduli of rigidity. If the square is much more rigid than the ground the peak pressure may be towards the edge; at the opposite extreme, it will be at the middle (or wherever the point mass is).