Mechanics (Statics) - Forces/Couples exerted by flexible bearings?

[vineroon]

Problem Statement
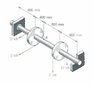
A steel shaft 120 mm in diameter is supported in flexible bearings at its ends. Two pulleys, each 500 mm in diameter, are keyed to the shaft. The pulleys carry belts that produce the forces shown. Determine the internal forces on a vertical section through point A.

I've been trying to start this problem, but the one thing I cannot figure out are what sort of forces are exerted at the ends of the shaft by the flexible bearings.

Also, I'm not sure why the diameter of the shaft would be required since it asks you to calculate the shear and axial forces along with the moment at cross-section A.

Any help would be greatly appreciated.

 

[Q_Goest]

Hi vineroon,
If the bearings weren't "flexible" could you do this problem?

The only 'flexible' bearings I'm aware of won't change the forces because the loads still need to be resisted in full. So try the problem again without consideration for flexibility in the bearing area.

 

[nvn]

vineroon: Each pulley has a resultant force and torque that is applied at the shaft axial centerline. Can you compute the resultant force and torque of each pulley and apply these at the shaft axial centerline? Now you have a beam problem, right? Actually, two separate beam problems and a torsion problem, which you could work separately, right? Why do you think they tell you the bearings are flexible? Does that tell you anything about the rotational constraint at the ends of your two beam problems?

Good observation on your part; the shaft diameter is not required for the given question.

 

[Dr.D]

I think perhaps this is telling you that the bearings are not fixed ends, that is, they are like ball-in-socket bearings. Thus the bending moment at the ends of the bearing span must go to zero.