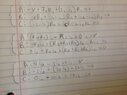madbo517
- 4
- 0
Howdy!
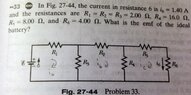
Looking for help with the following problem (#33). I found it easiest to take a picture of the problem statement and the figure and another of my work (I am working on learning LaTeX so I can write them neatly in posts, but until then, I hope a picture is sufficient).
I got the system of 3 formulas in the picture, but in all the practice ones we did, we were given V, in this problem we're given one of the currents, but I'm not sure how to use that in this problem.
I'm using mesh currents (ia, ib, and ic), because that's how these types of problems were explained to us, although I'm sure there are multiple methods to solve this problem.
Thanks for the help!
Looking for help with the following problem (#33). I found it easiest to take a picture of the problem statement and the figure and another of my work (I am working on learning LaTeX so I can write them neatly in posts, but until then, I hope a picture is sufficient).
I got the system of 3 formulas in the picture, but in all the practice ones we did, we were given V, in this problem we're given one of the currents, but I'm not sure how to use that in this problem.
I'm using mesh currents (ia, ib, and ic), because that's how these types of problems were explained to us, although I'm sure there are multiple methods to solve this problem.
Thanks for the help!